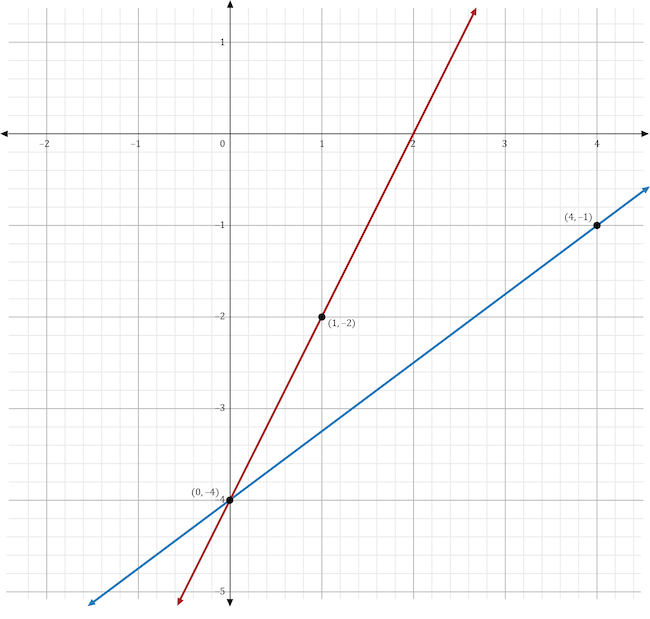Perfect Tips About Does A Linear Curve Have Constant Slope How To Change The Scale On Excel Graph
![What is Constant vs Variable Slope of a Function? [853] YouTube](https://cdn-academy.pressidium.com/academy/wp-content/uploads/2021/08/Changing-Constants-in-Graphs-of-linear-functions.png-2.png)
When the curve is approximated by a series of points, the slope of the curve may be approximated by the slope of.
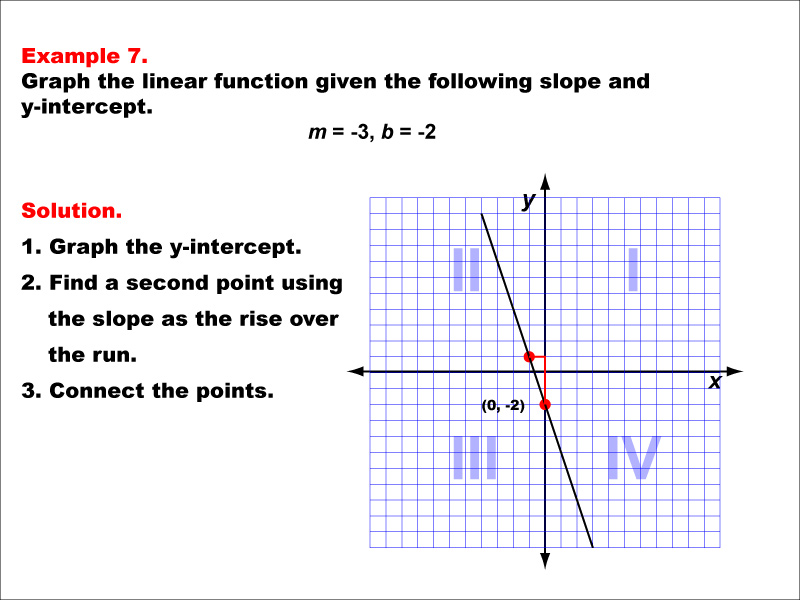
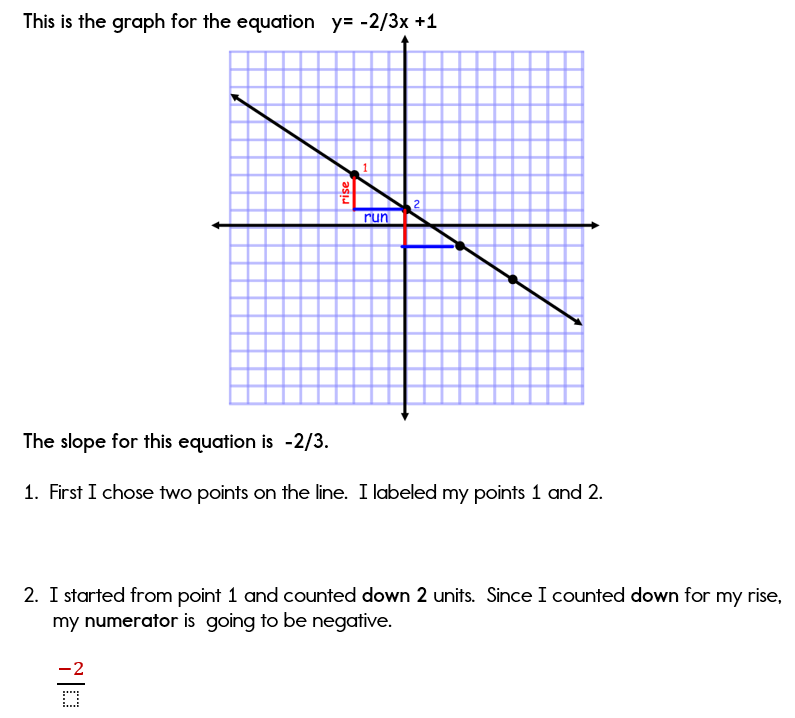
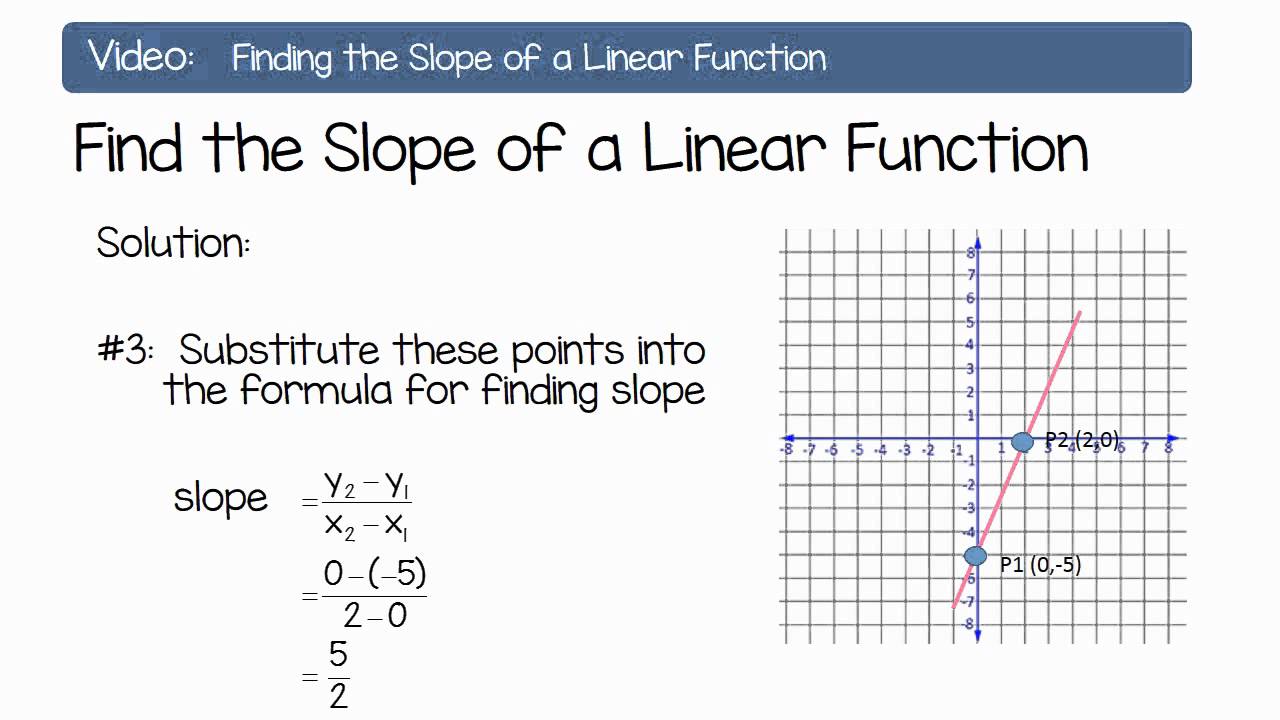
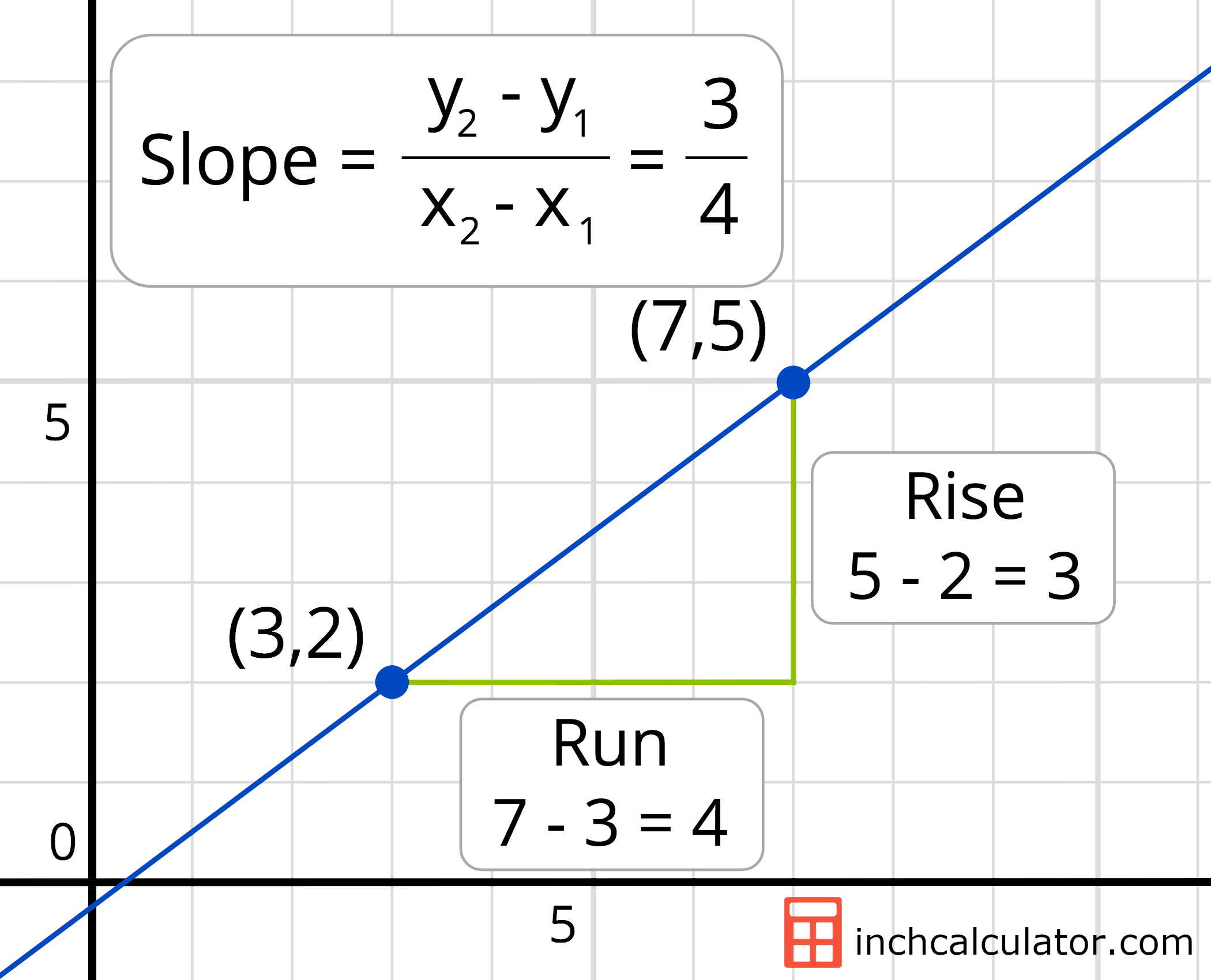
Does a linear curve have a constant slope. Divide the change in height by the change in horizontal distance. Here are some good things to know: If you are not given 2 points, you can find 2 points on the graph and use them to find the slope.
B is the slope of the line. What is the slope at some point such as p? Graphing a function by plotting points.
The equation of a vertical line is x=0 or x=1 or x=some constant. Learn how to write the slope formula from scratch and how to apply it to find the slope of a line from two points. Use transformations of the identity function f(x) = x f ( x) = x.
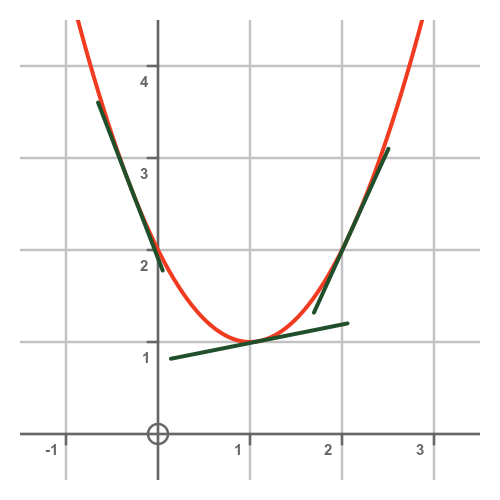
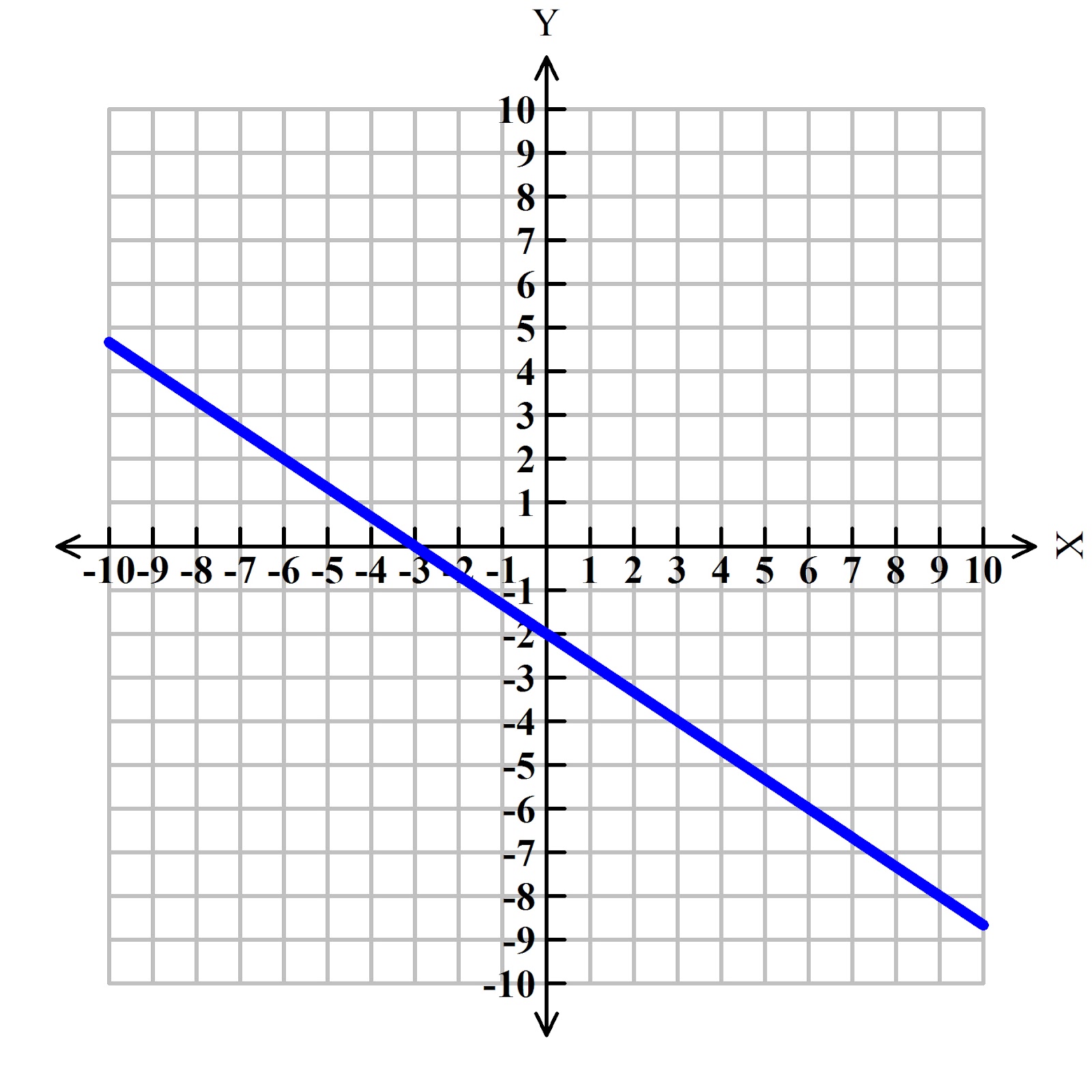
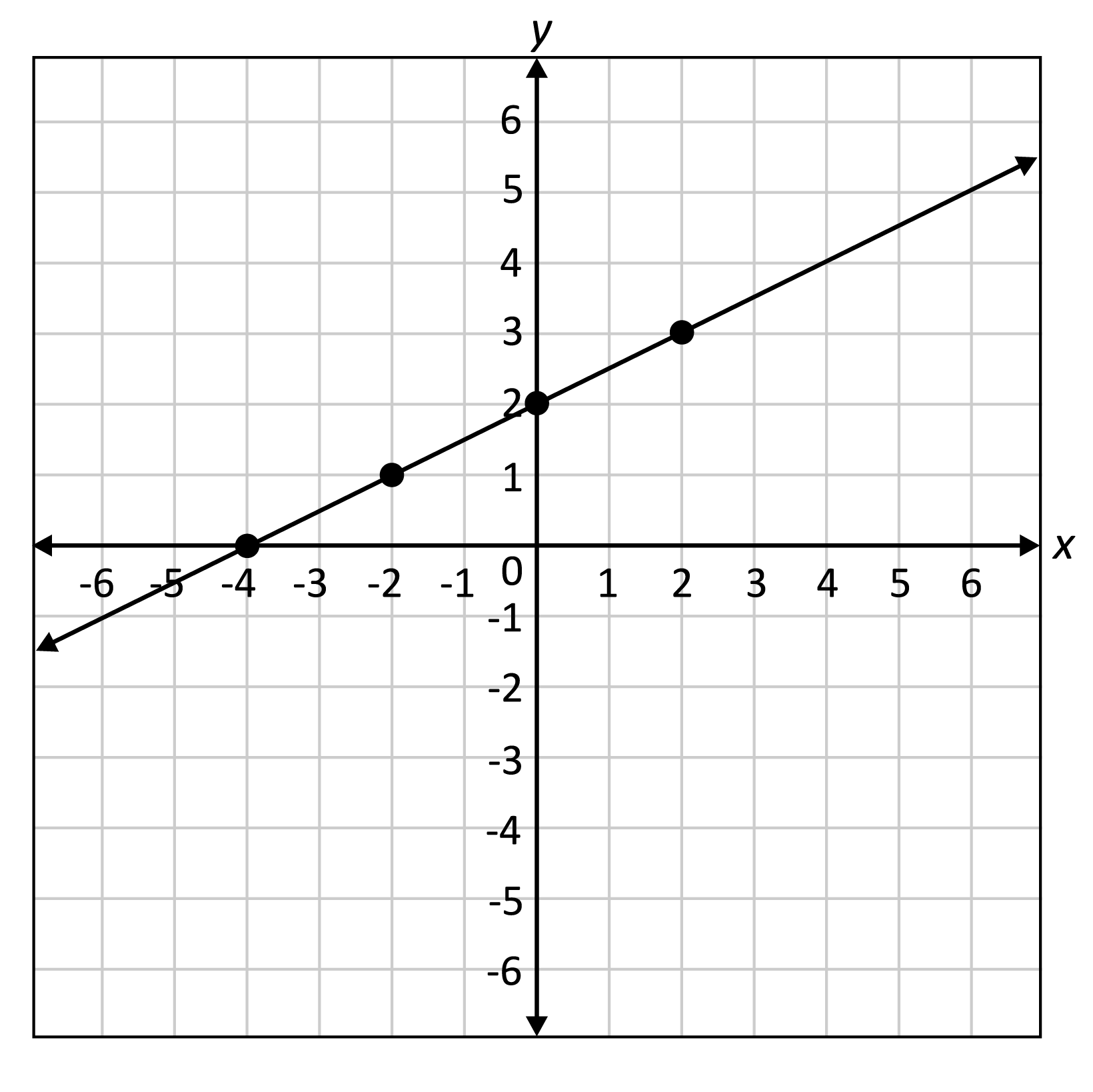
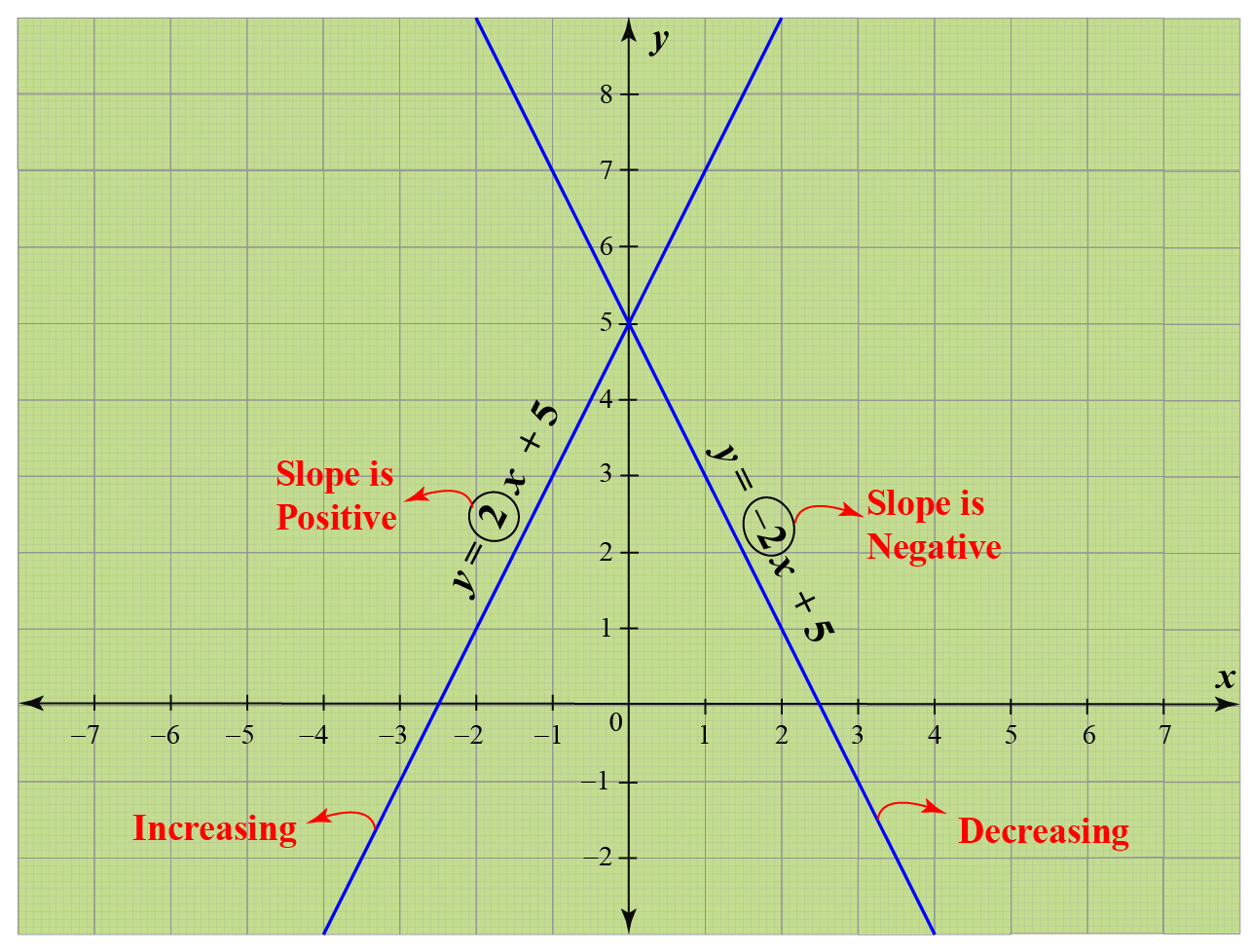
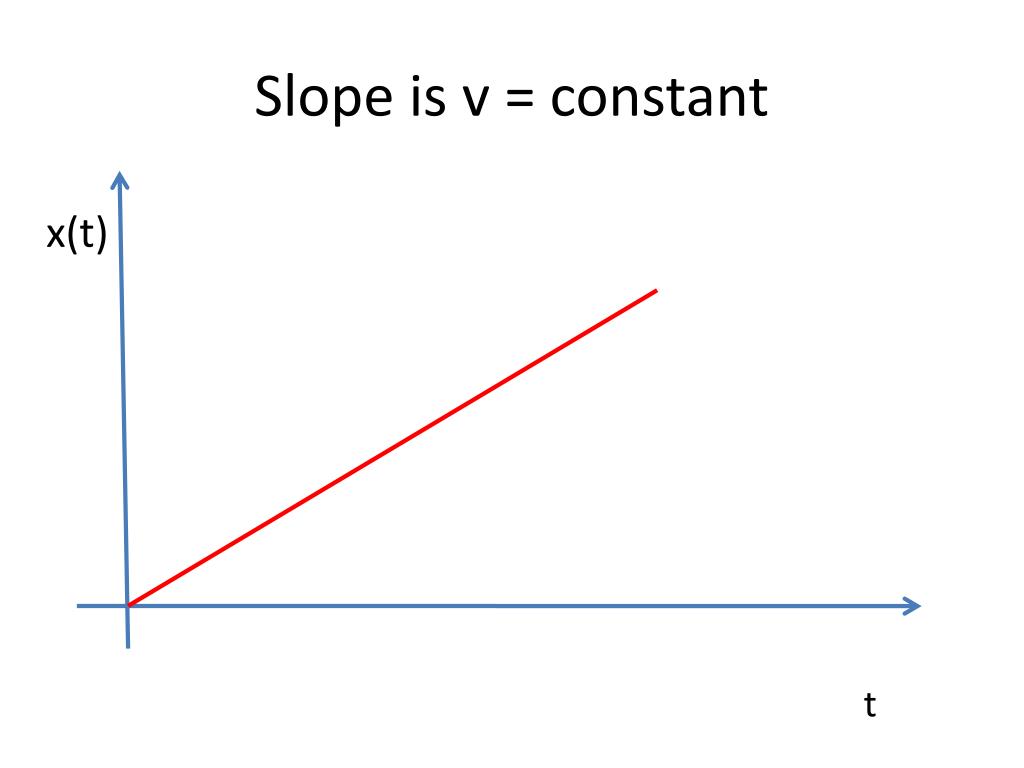
The slope of a line is usually represented by the letter m. (p can be at any point along the curve.) it can be seen that the slope of the function depends on the position of p on the curve. A constant slope denotes a straight line.
You can always figure out the slope of a line if you have 2 points. Consider the linear function: Hence, a linear graph looks like a straight line.
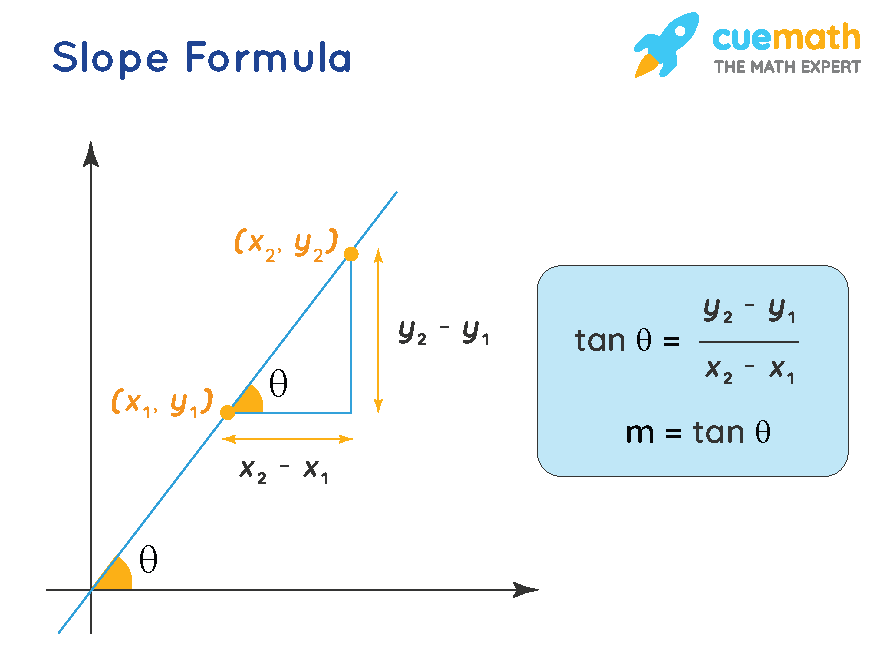
The gradient (also called slope) of a line shows how steep it is. Price elasticity of supply and the slope of the supply curve By stretching a rubber band between two pegs on a geoboard, we can discover how to find the slope of a line.
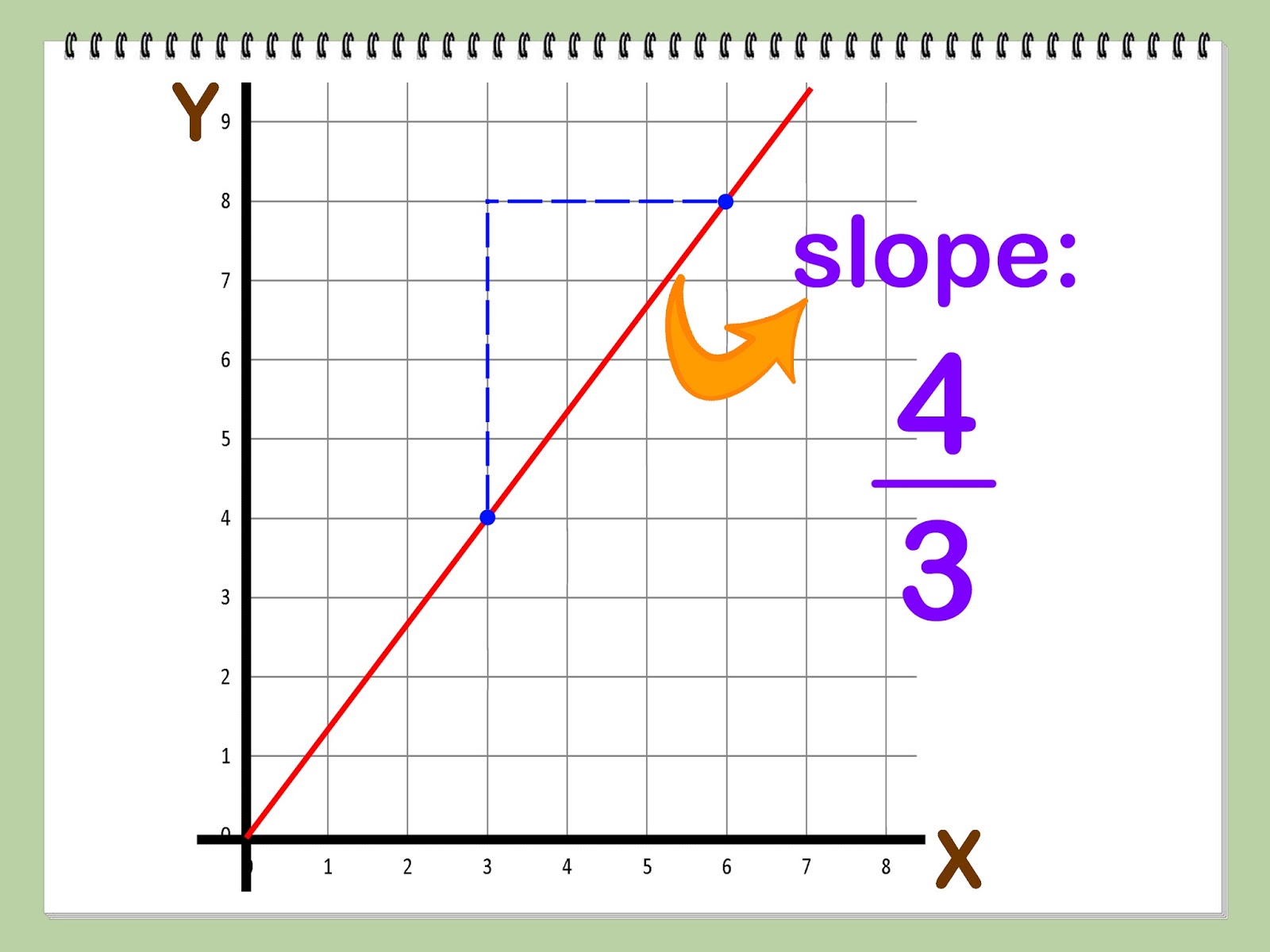
If written with a y in the equation, x=1 becomes. One characteristic of a line is that its slope is constant all the way along it. Slope = change in y/change in x = rise/run.
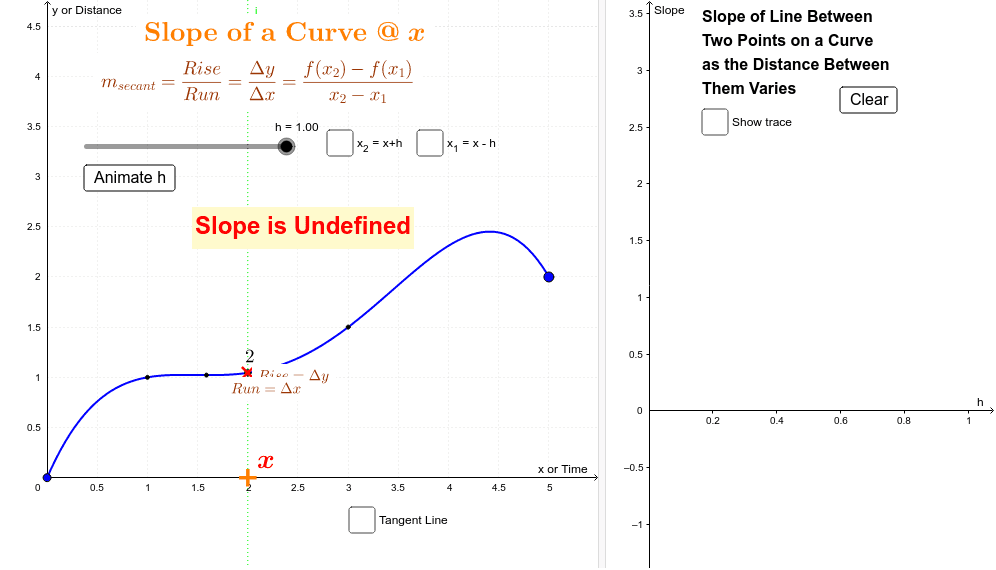
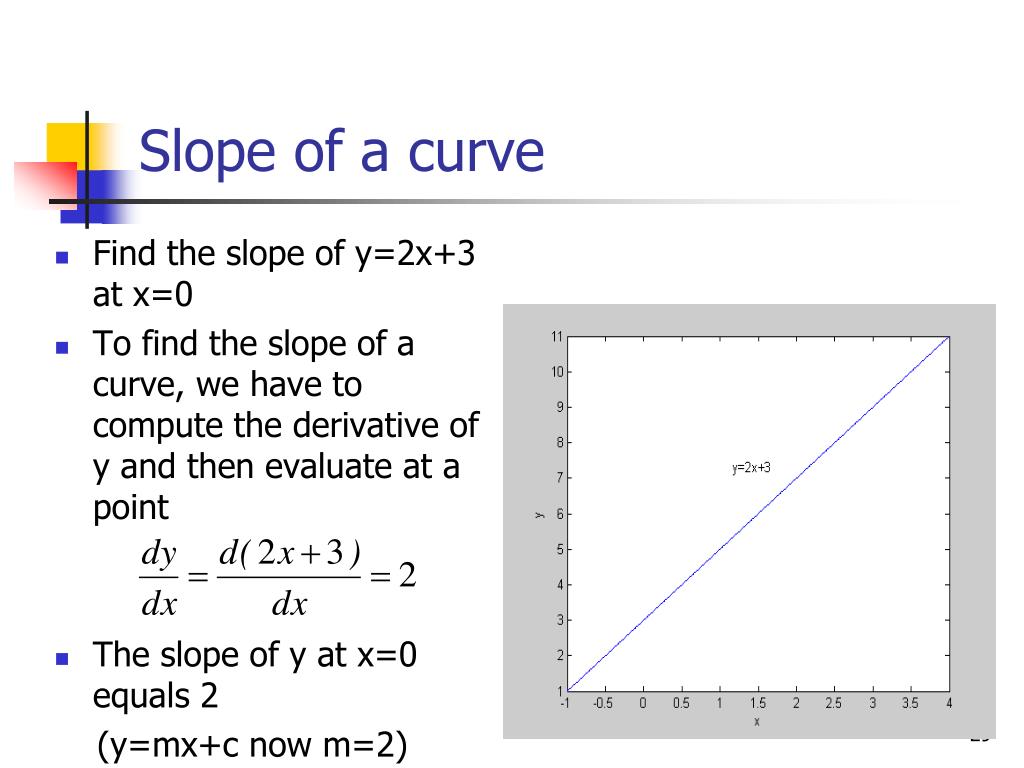
This form of the equation is very useful. The slope can also tell you information about the direction of the line on the coordinate plane. Finding the slope of a curve at a point is one of two fundamental problems in calculus.
Doing the manipulative mathematics activity “exploring slope” will help you develop a better understanding of the slope of a line. The problem is to find the slope of the function at point p. Generalizing this, differential calculus defines the slope of a curve at a point as the slope of its tangent line at that point.
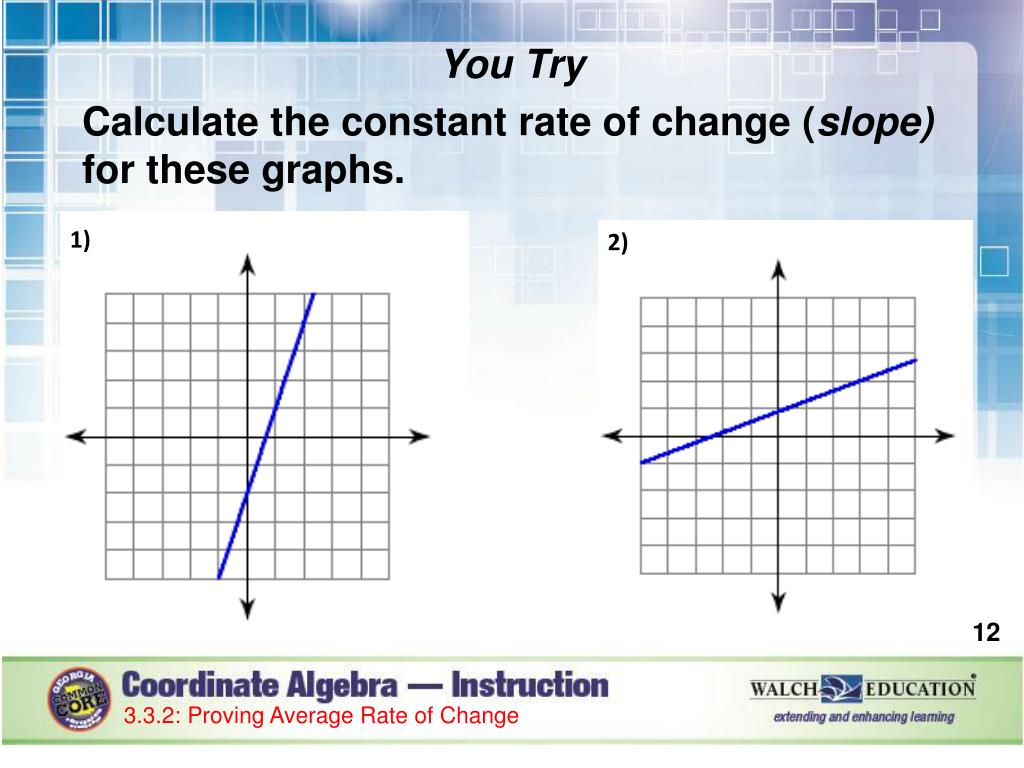
Slope can be calculated either by looking at the graph of a line or by using the coordinates of any two points on a line. It is possible, however, for a demand curve to have constant price elasticity of demand, but these types of demand curves will not be straight lines and will thus not have constant slopes. This abstract concept has a variety of concrete realizations, like finding the velocity of a particle given its position and finding the rate of a reaction.

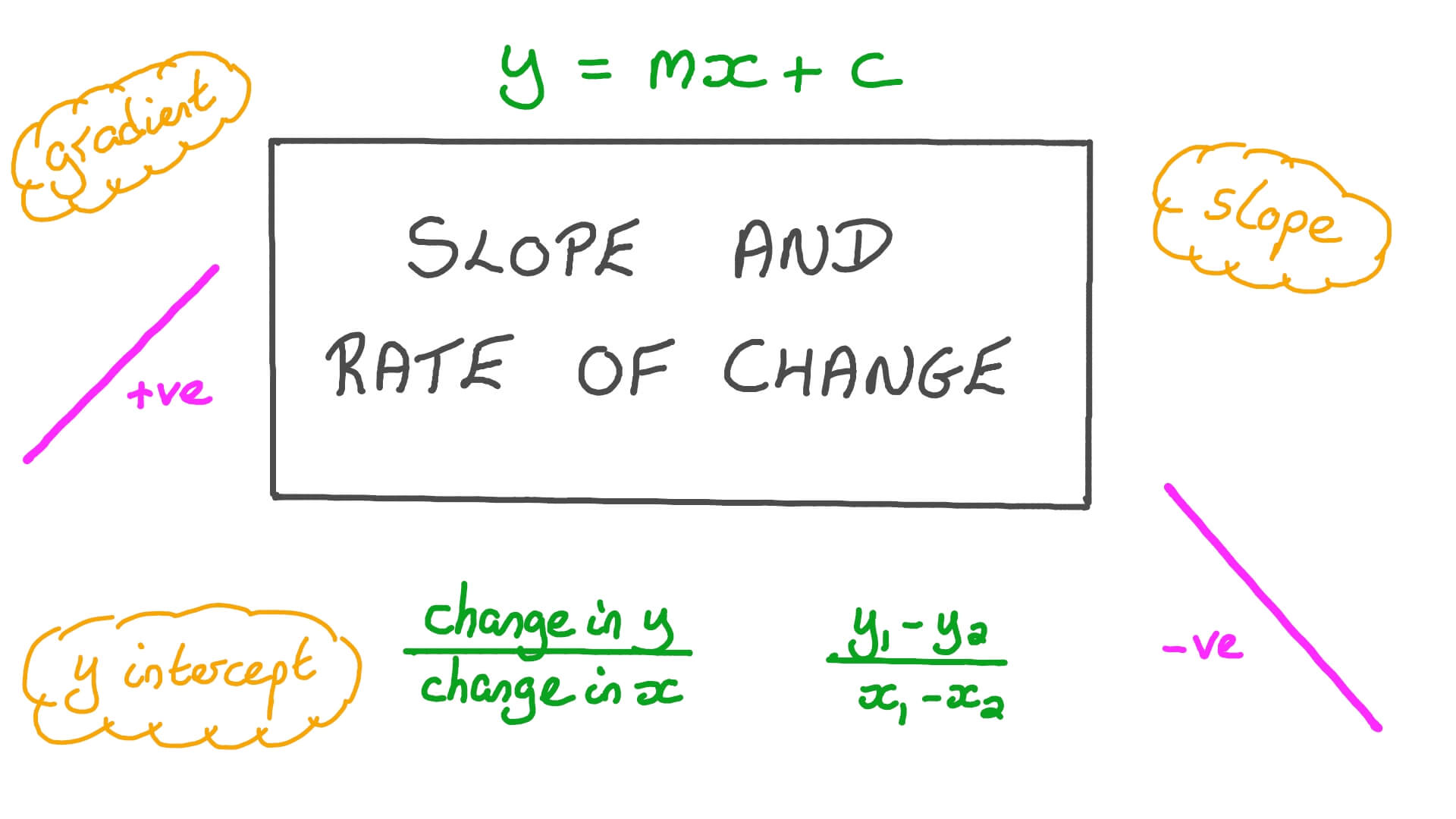
![What is Constant vs Variable Slope of a Function? [853] YouTube](https://i.ytimg.com/vi/7Eqso7Isztg/maxresdefault.jpg)