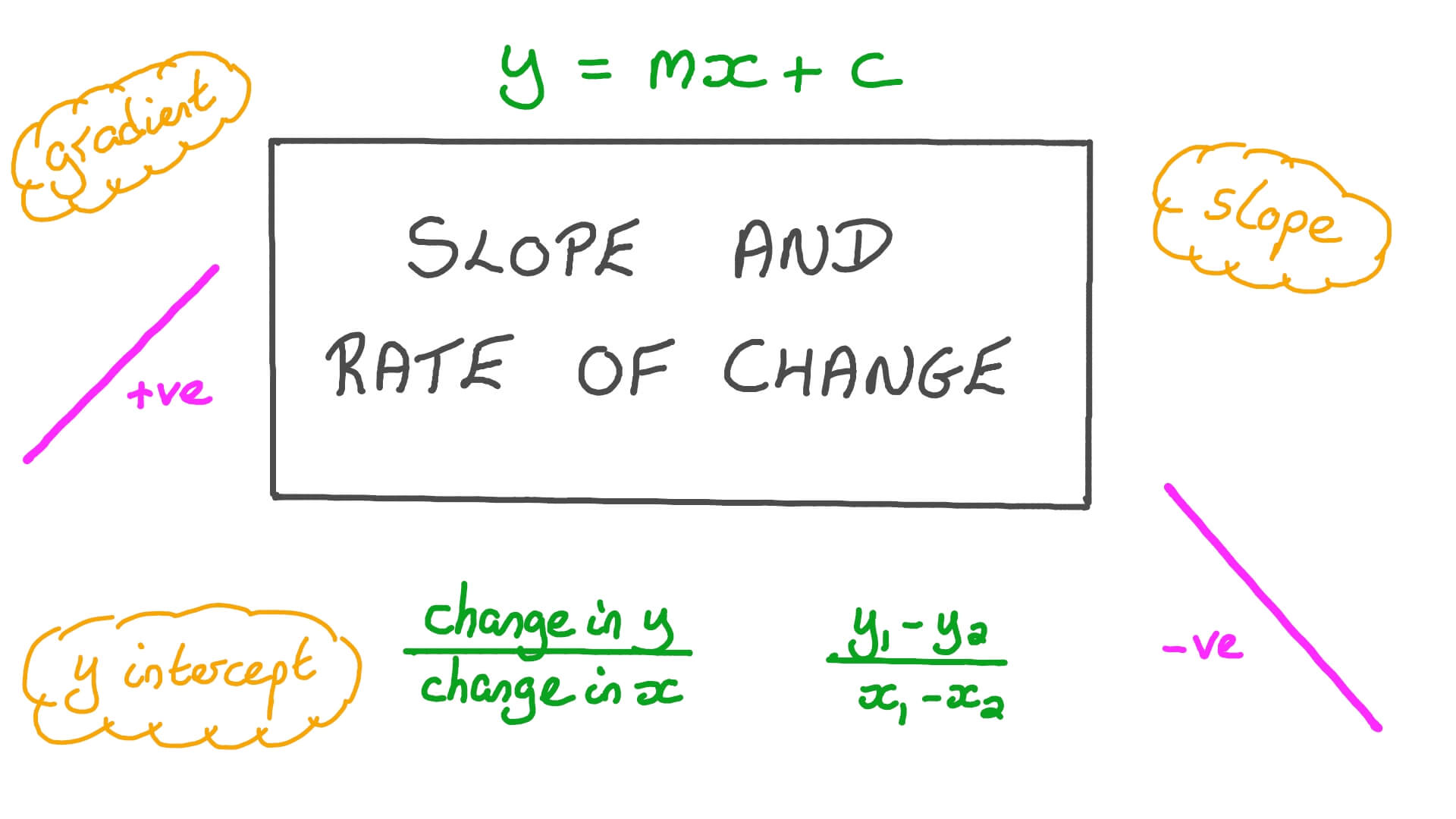One Of The Best Tips About Does The Slope Of A Curve Change Excel Data From Horizontal To Vertical

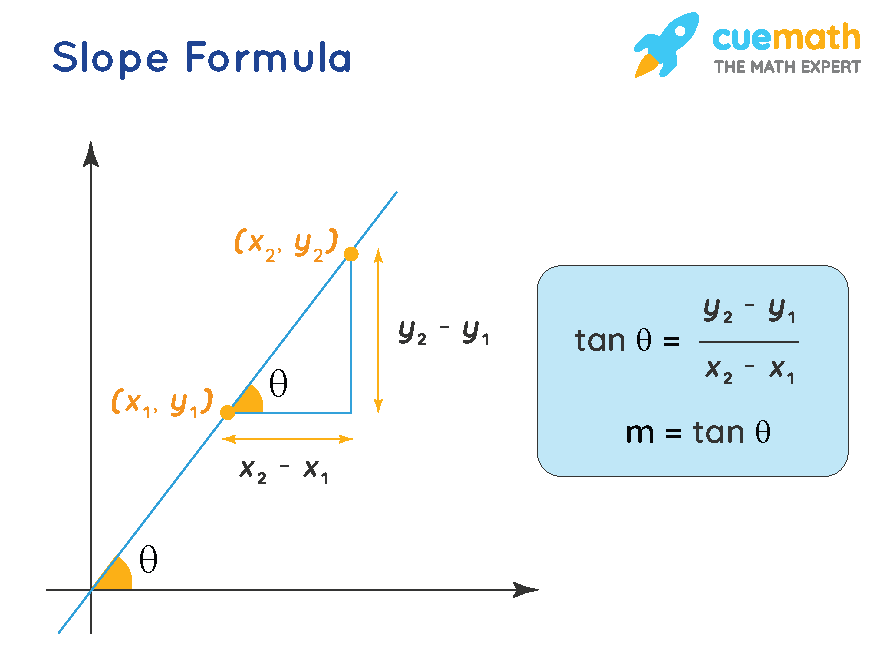
For a line of the form (or any other form) \(y=mx+c,\) we can find its slope by simply taking any two values of \(x,\) \({x}_{1}\) and \({x}_{2},\) and their respective \( y\) values, \({y}_{1}\) and \({y}_{2}\).

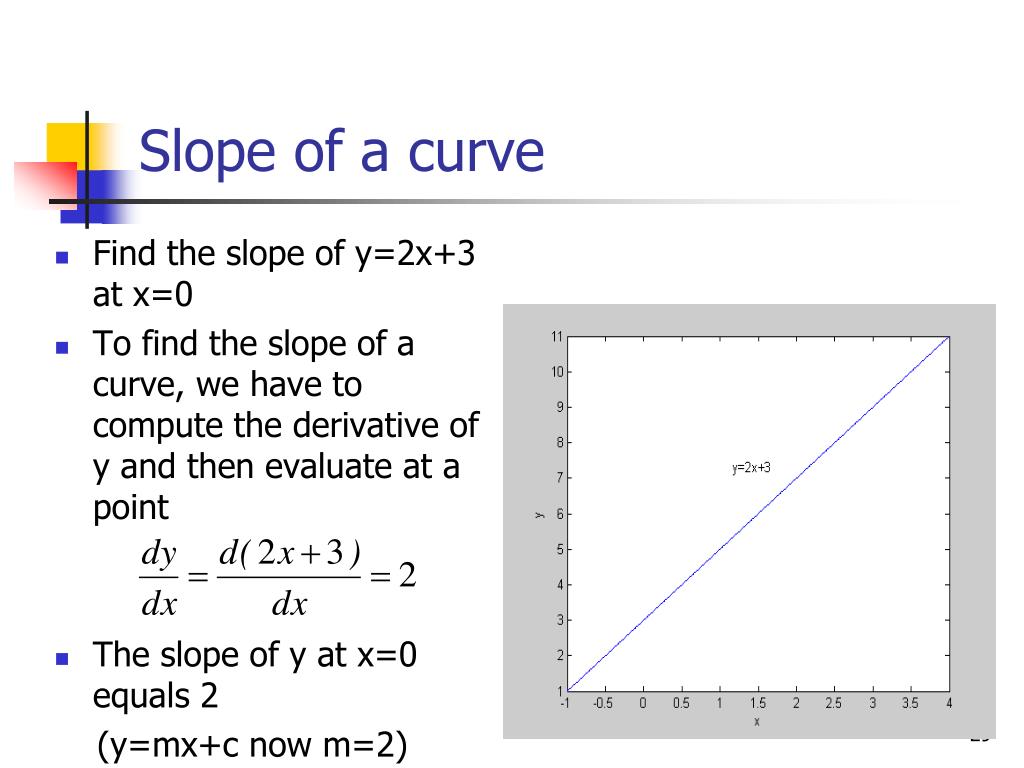
Does the slope of a curve change. X = 11.4 y = 11.5. We will choose the point where x = 2. We'll explore how to use this powerful tool to determine the equation of the tangent line, enhancing our understanding of instantaneous rates of change.

So let's start by choosing a particular point on the curve. More precisely, using big o notation, one has. When the curve is approximated by a series of points, the slope of the curve may be approximated by the slope of.

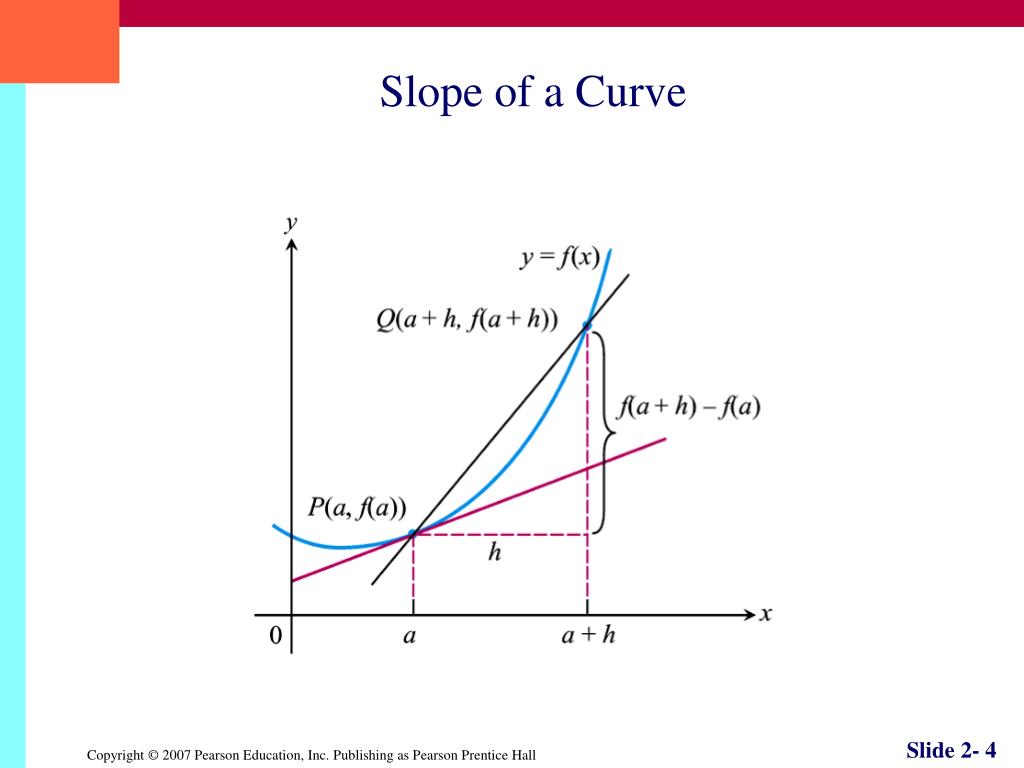
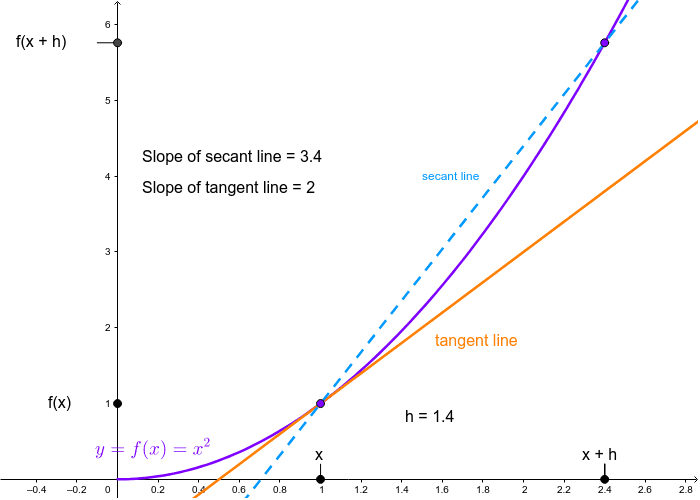
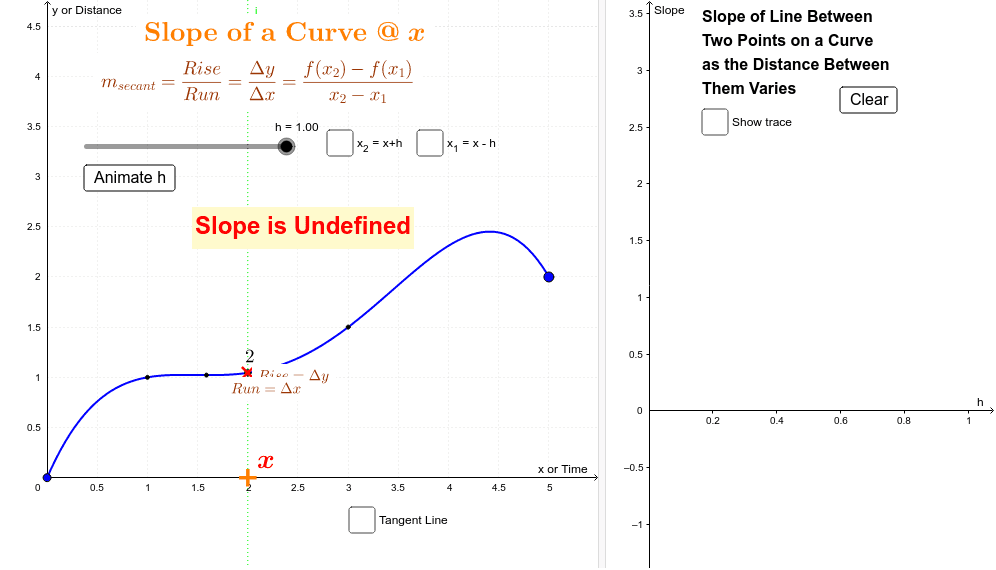
The slope of the secant line is the average rate of change of \(f\) over the interval \(x_{0} \leq x \leq x_{0}+h\) So, all we need to do is find the slope of the line through the. The same dy/dx can also be defined as the slope of a curve at some value of x.

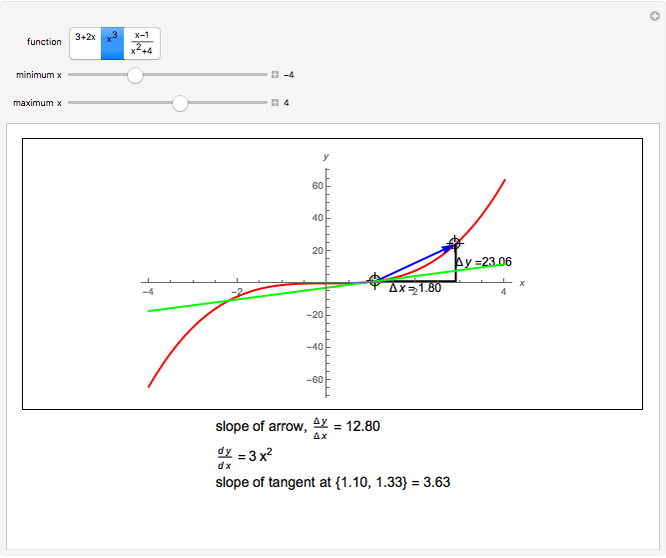
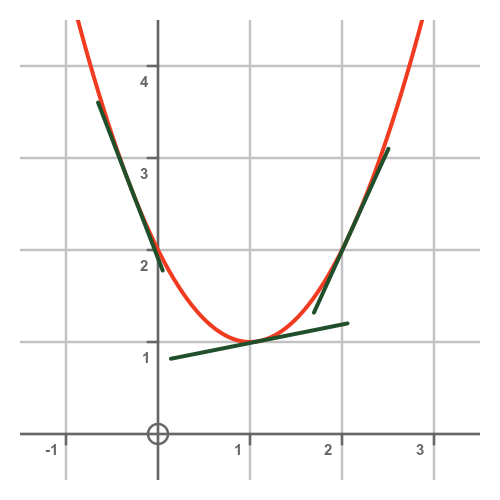
Mathematically, the slope of a curve is represented by rise over run or the change in the variable on the vertical axis divided by the change in the variable on the horizontal axis. Slope to the right of the origin? We can clearly see that the slope of the curve is changing;

Is small, the signed curvature is well approximated by the second derivative. That means that the slope is increasing. The slope (also called gradient) of a line shows how steep it is.

But i just like to think of it as rise over run. The rise measures the vertical change and the run measures the horizontal change when moving from one point on the line to another on the line. This can be interpreted as a measure of sensitivity'';

The first thing to realize is that each solution is a point on the line. To find the slope of the line, pick two points on the line. Let's say we've looked at our graph, and have picked the points (3, 2) and (5, 6).

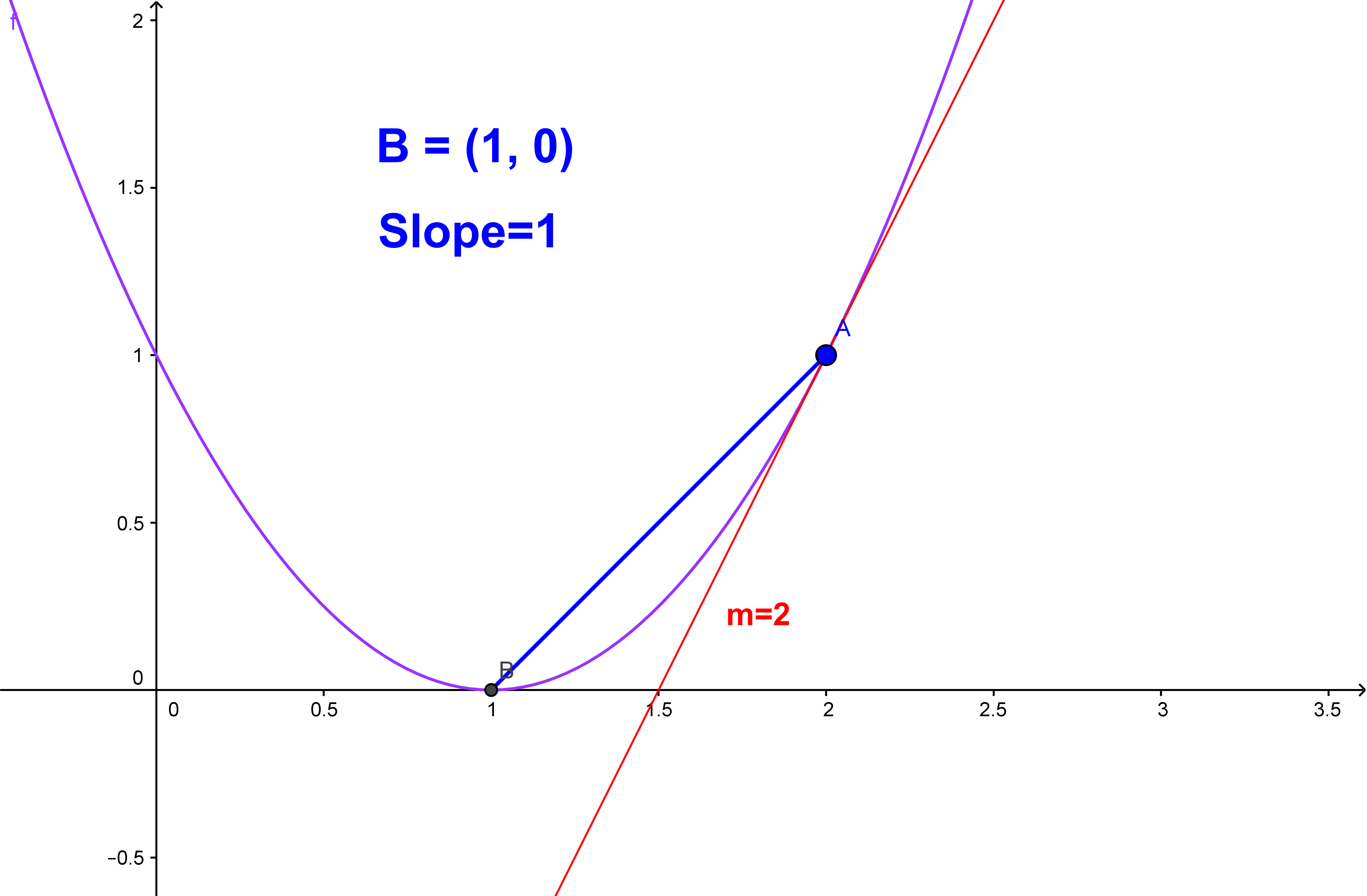
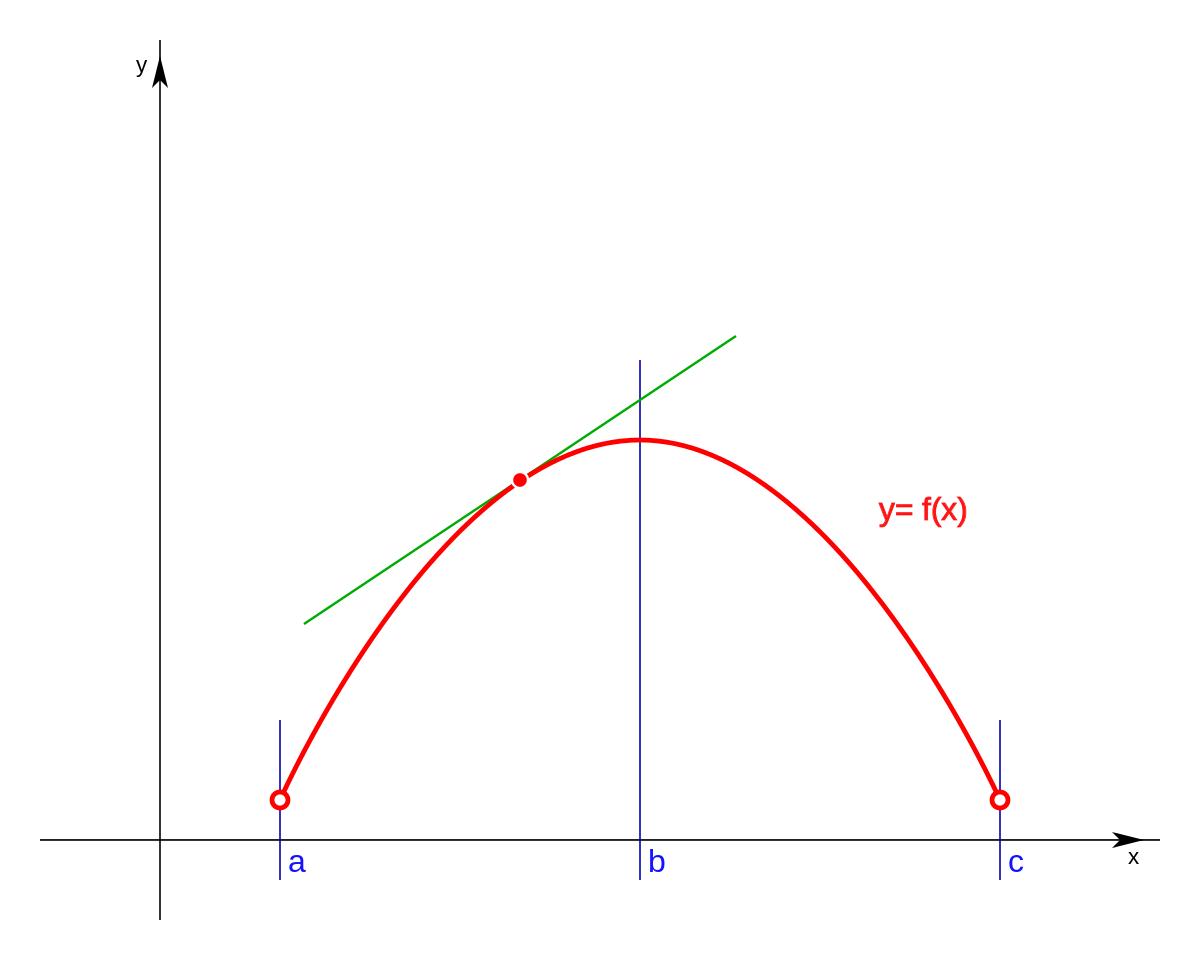
We can clearly see that the curve becomes steeper and steeper as $x$ increases. Discover how the derivative of a function reveals the slope of the tangent line at any point on the graph. The slope of a curve at a point is equal to the slope of the tangent line at that point.

In technical terms, the slope of the line is the change in y over the change in x. Hence, it is a curve. When the slope of the graph.

The slope of a line is \(m=\dfrac{\text{rise}}{\text{run}}\). Geometrically, the average rate of change is represented by the slope of a secant line (figure a, below) and the instantaneous rate of change is represented by the slope of the tangent line (figure b, below). Have a play (drag the points):