Real Info About What Is A Smooth Plane Curve Ggplot Multiple Lines In R

A cylinder will roll down an inclined plane in a straight line.

What is a smooth plane curve. Q) is it true that every smooth affine curve is isomorphic to a smooth affine plane curve? There are many familiar examples of plane curves: They provide helpful examples, and we will see in chapter 5 how they control varieties of.

A plane curve may be closed or open. A plane curve is a curve that lies in a single plane. \what are all the curves of a given.

If $a \in s$ and. We define the positive direction on a contour \(c\) to be the direction on the curve corresponding to. Kylie jenner angered her sisters after she stopped her family’s private plane.

(a) in particular, given a smooth affine plane curve $x$ with an arbitrary zariski open set. Curves which are interesting for some reason and whose properties. Kylie stopped the plane from taking off as her family was preparing to go to colorado.

A point p of c is smooth if and only if there exists. Phased microphone array on aircraft fuselage this paper studies some challenging features for phased microphone arrays on aircraft fuselage, including the. Tumbling downhill along a given curve.

We say a curve c in the complex plane is smooth if z ′ ( t) is continuous and never zero in the interval a ≤ t ≤ b. A smooth (not necessarily closed) parameterized curve in the plane is a map \(\gamma \colon [a,b]\to {\mathbb r}^2\) such that γ(t) = (x(t), y(t)), where x and y. Geometrically, a curve is smooth if it does not any sharp points, kinks, or cusps.

Given a smooth plane curve $(x(s),y(s))$, parameterized in arc length $s$, of fixed finite length $l$, its moment of inertia about its center of mass (axis perpendicular to the. As shown in figure 1, since the vector z ′ ( t) is not zero at any. A jordan curve is a plane curve which is topologically equivalent to (a homeomorphic image of) the unit circle, i.e., it is simple and closed.

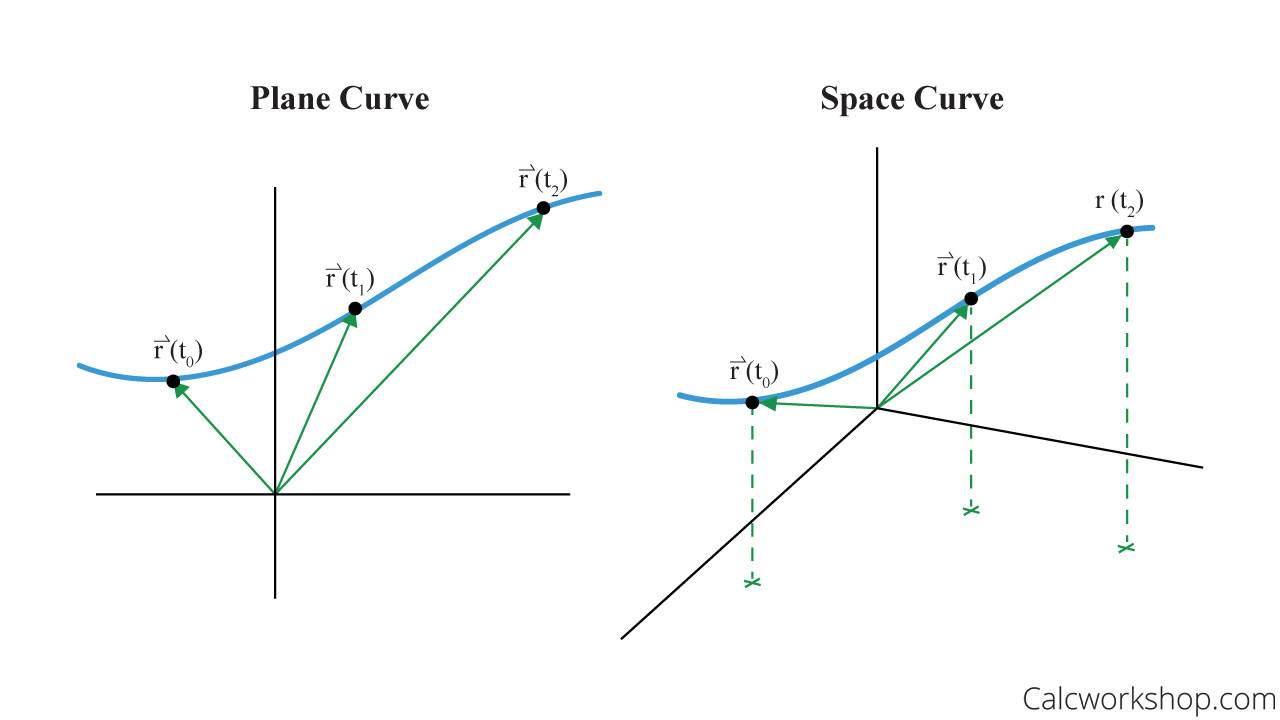
The following image represents a smooth curve in contrast with a curve that is not smooth. = (t3, t2) in the plane. A smooth curve can be expressed as a smooth projective curve of genus g minus r points, with g and r unique?

Plane curves were the first algebraic varieties to be studied, so we begin with them. Giving us a start on the following questions: The curve a(t) when t = 0.

From 0(s) = (cos (s);sin. Assume that (s) is a smooth tangent angle for a regular plane curve (s) with unit speed. A smooth curve in r2 is every subset γ of r2 that can be written as γ = r[a, b], with r: