Neat Tips About How Do You Know If A Slope Will Be Positive Or Negative Velocity Time Graph Acceleration
Student Tutorial Slope Concepts Definitions Media4math How To Label X And Y Axis In Excel Find Point Graph
Slope Brilliant Math & Science Wiki How To Switch Horizontal And Vertical Axis In Excel Graph Multiple Lines
How To Know If The Slope Is Negative Or Positive Create X And Y Axis In Excel Add Target Line Stacked Bar Chart
Undefined Slope Vs Zero Negative Positive Rise Add Trendline To Bar Chart Tableau Create A Line Sparkline
Coordinate Geometry (solutions, Examples, Games, Questions, Videos) Mermaid Horizontal Graph D3 Line Chart Multiple Lines
Ppt Equations Of Lines In The Coordinate Plane Powerpoint Charts Js Line Chart Excel Add Dots
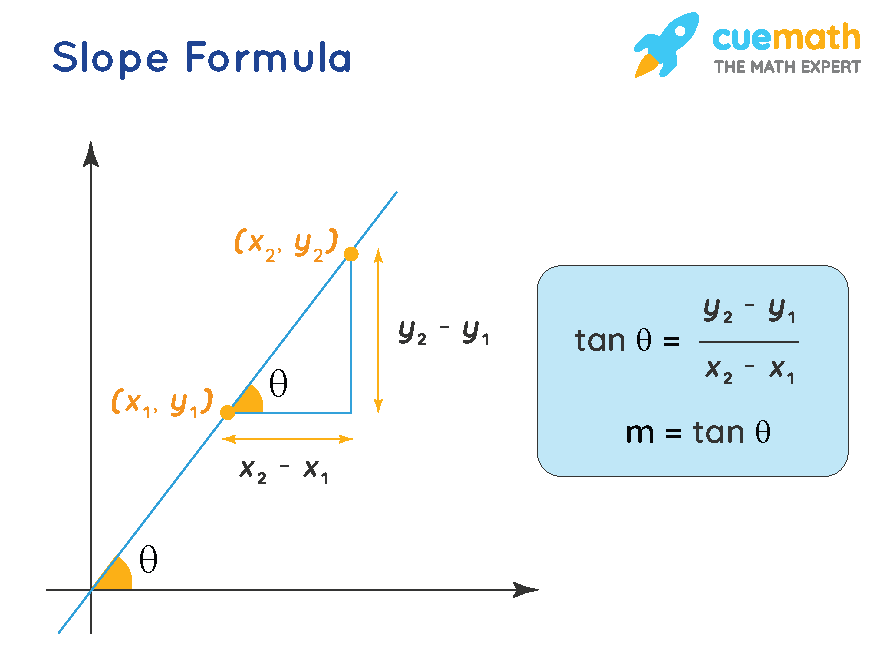
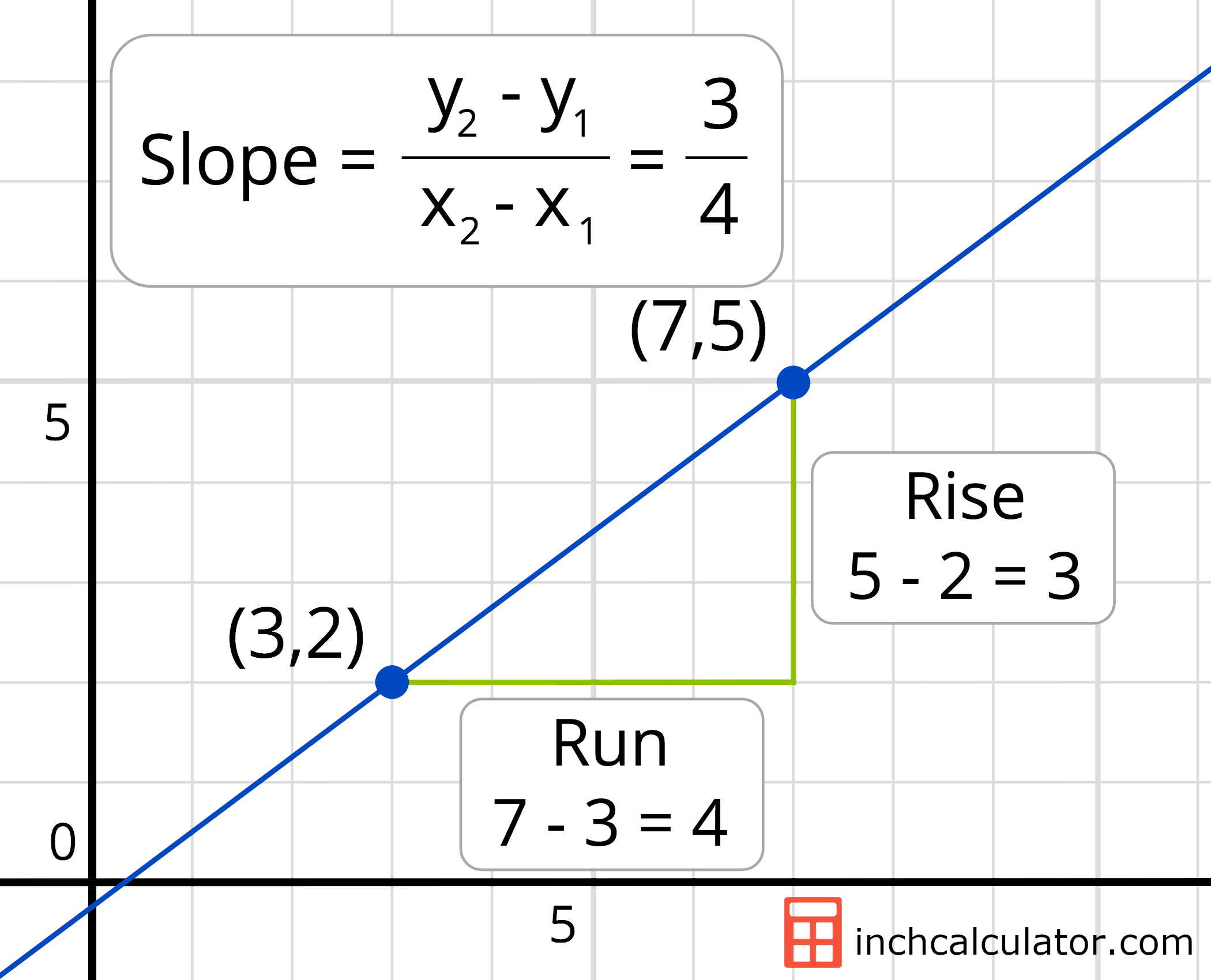
We can find the slope between any two points on a line, and it's always the same.
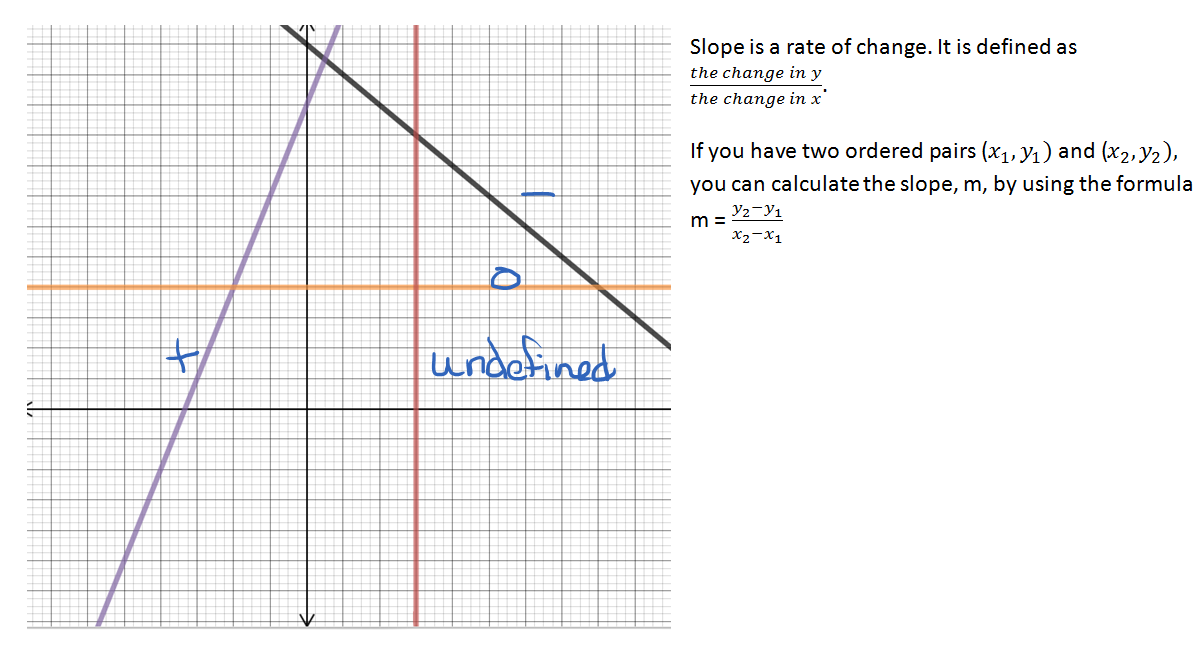
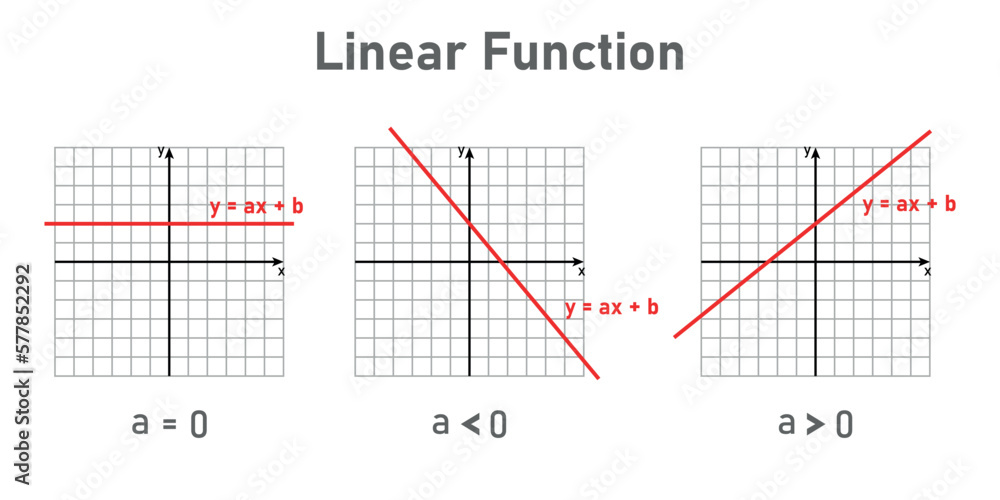
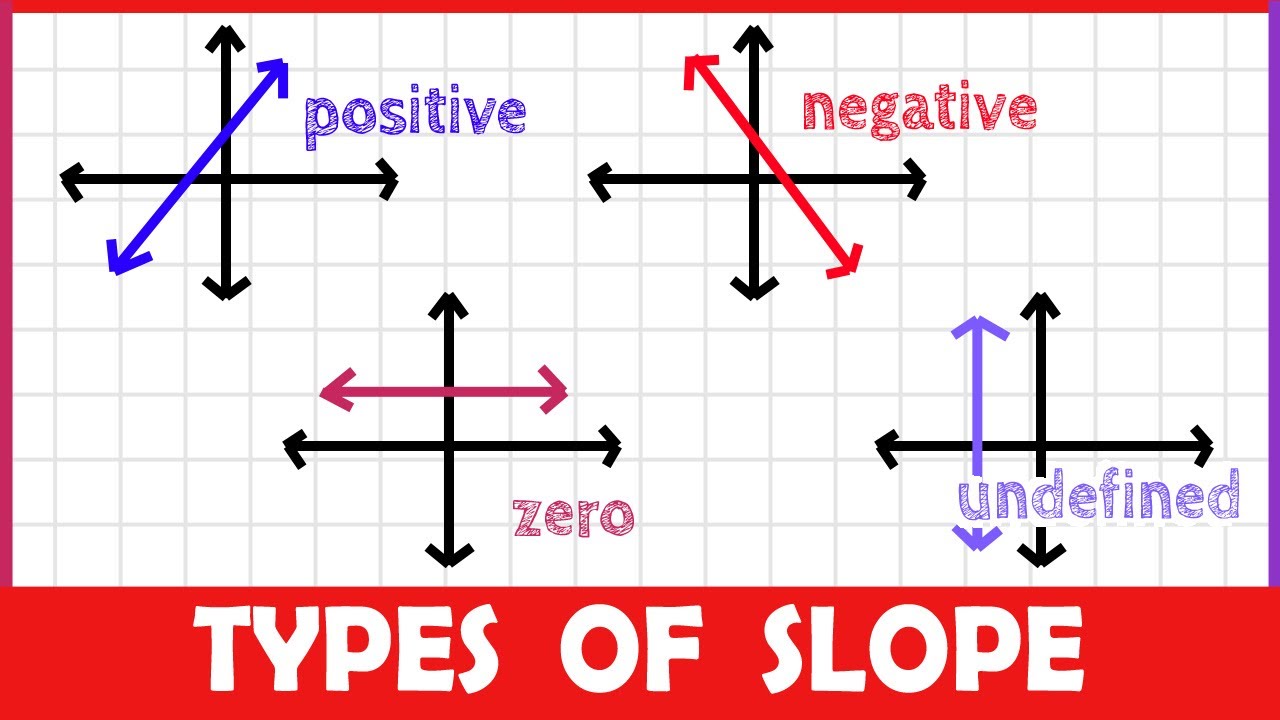
How do you know if a slope will be positive or negative. If we go down, it's negative. Positive, negative, zero, plus the undefined slope. Do you notice any difference in the two lines shown in figure (a) and figure (b)?
Explore the different types of slopes of a line: In this article, we are going to discuss what a slope is, slope formula for parallel lines, perpendicular lines, slope for collinearity with many solved examples in detail. Algebra is the language through which we describe patterns.
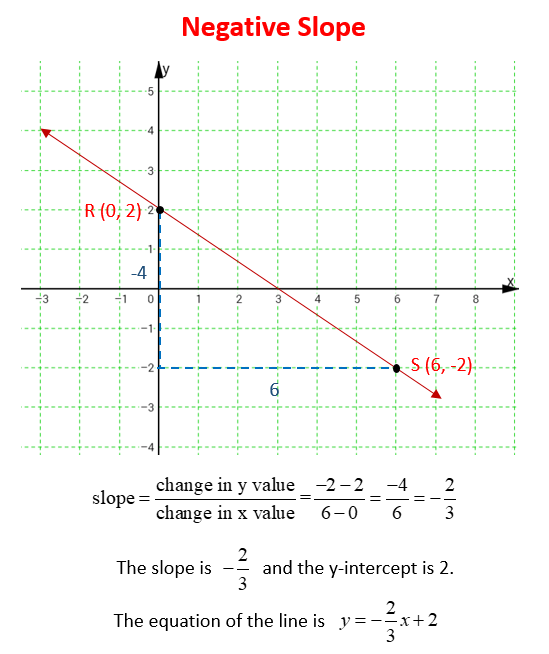
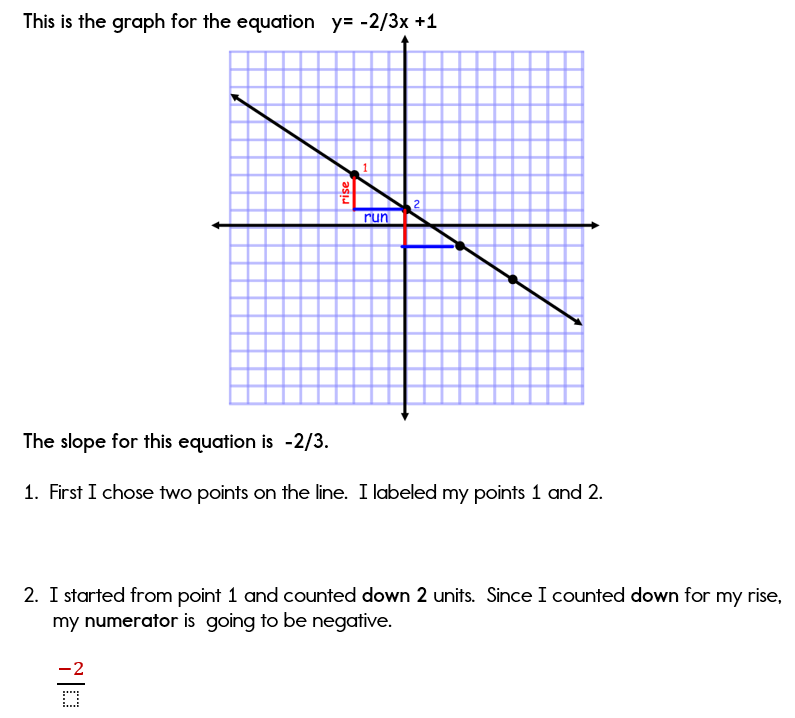
How to tell if a graph is positive or negative. Use the formula for slope to define the slope of a line through two points. Slope = −4 2 = −2.
When the slope is a positive number the line goes up from left to right. That is, if you are moving in a positive or negative direction. Find the slope of the lines [latex]x=a [/latex] and [latex]y=b [/latex] recognize that horizontal lines have slope = 0.
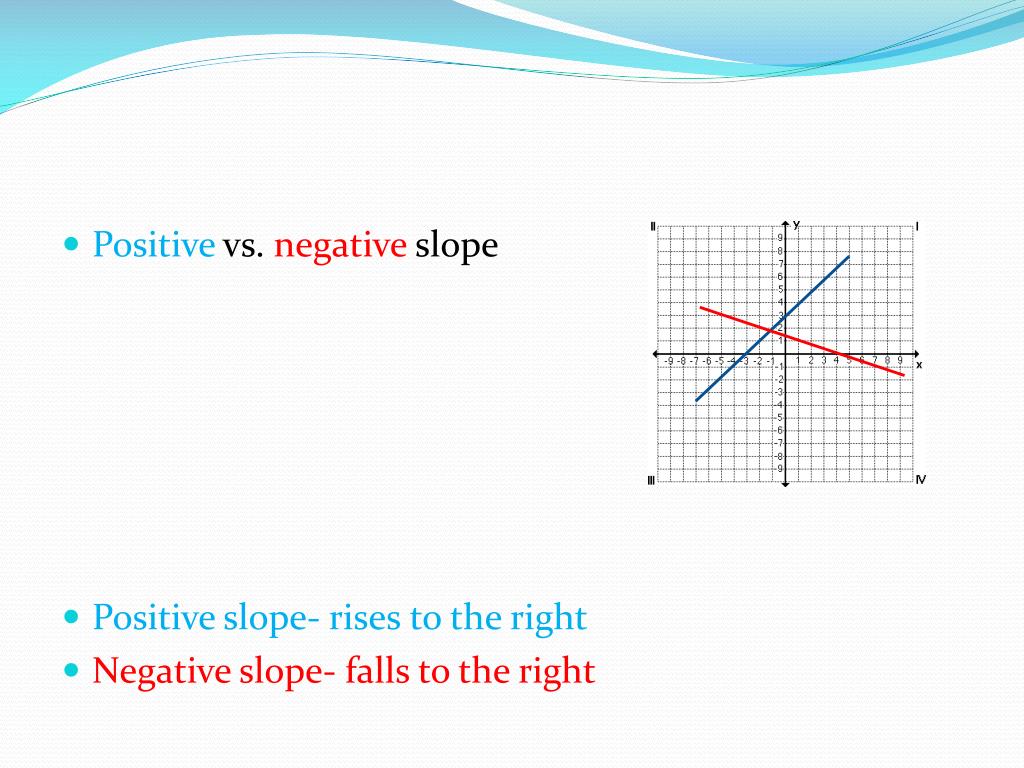
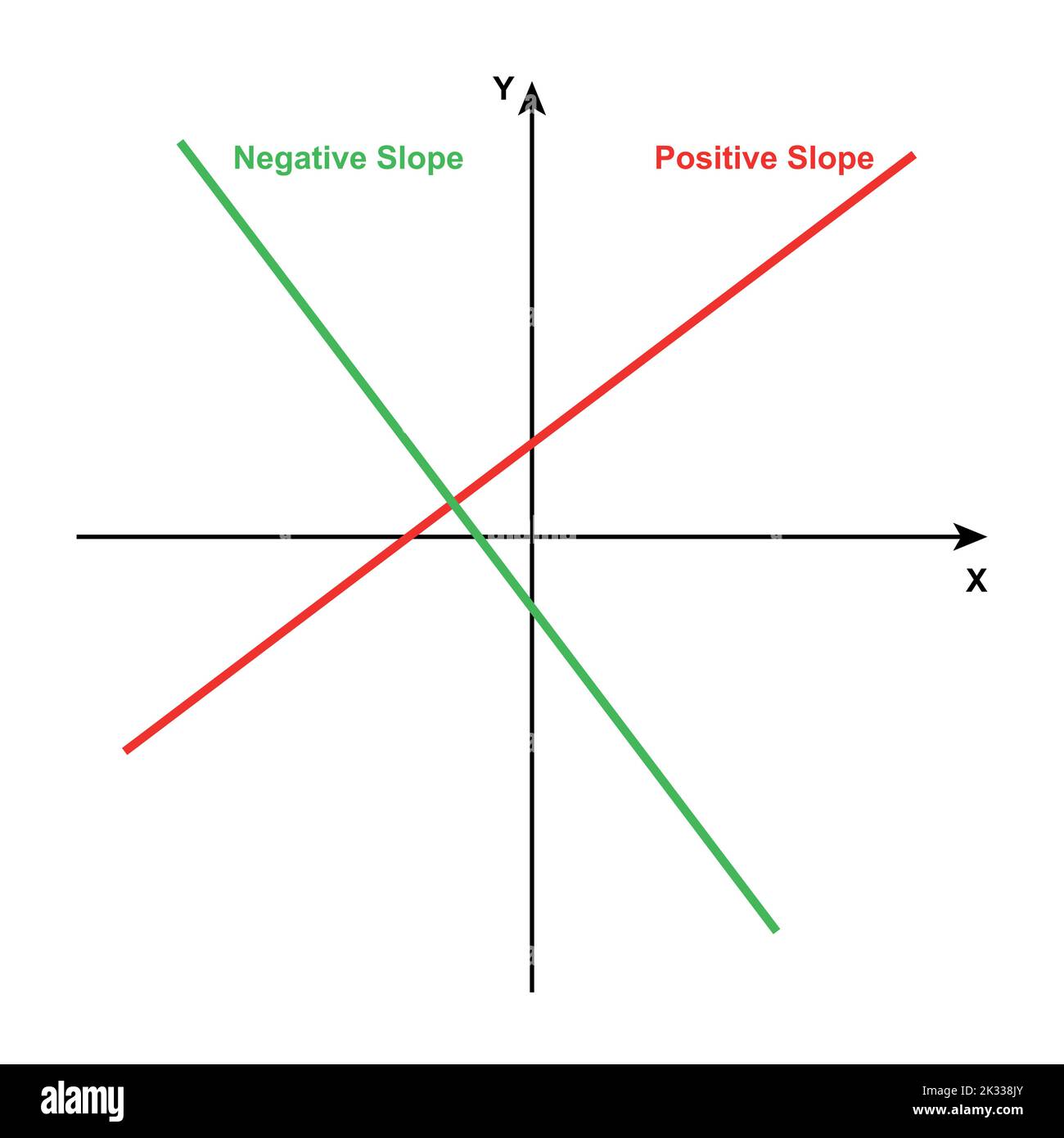
This relationship between the sign on the slope and the direction of the line's graph can help you check your calculations: A negative slope means y decreases as x increases (visually, the line moves down as you go from left to right). That line goes down as you move along, so it has a negative slope.
If slope is negative, then the line moves down as we move right (y decreases as x increases). If slope is zero, then the line moves neither up nor down as we move right (y is unchanged as x increases). Think of it as a shorthand, of sorts.
Slope can be positive or negative depending on if the line is vertically higher on the left or on the right. M = = = 2. (but going across to the left is negative).
Positive linear graph: If slope is positive, then the line moves up as we move right (y increases as x increases). If you go up to get to your second point, the rise is positive.
A zero slope means that y is constant and does not change as x changes. In the function y = 3 x, for example, the slope is positive 3, the coefficient of x. Let's use the slope formula to find the slope of the line that goes through the points ( 6, − 3) and ( 1, 7).
Up is positive, and down is negative. Distinguish between graphs of lines with negative and positive slopes. As opposed to having to do something.
Graphing Slope Systry Add Line To Chart Excel Google Data Studio Trend
Ex 1 Determine The Slope Given Graph Of A Line (positive Power Bi Dual Axis Chart Adding Vertical In Excel
Slope Formula What Is Formula? Equation, Examples En How To Make A Curved Line Graph In Word Contour Plot R Ggplot
Slope Of Straight Line On Cartesian Coordinate. Positive And Negative Ti 84 Plus Ce Best Fit Interactive Graph
Como Calcular El Slope Printable Templates Free Excel Chart Add Secondary Axis Lucidchart Draw Line
Negativeslope Seaborn Scatter Plot Regression Line Average In Excel Chart
Positive And Negative Slope Algebra I Ggplot Stacked Area Plot Add Line To Excel Chart
Positive And Negative Slope Graph Stock Vector Image & Art Alamy Draw Regression Line In Python How To Create Excel
Calculating Slope Add Drop Lines To Excel Chart Cumulative Line Graph
Positive Slope Math Definition Christine Engen's Worksheets Chart Trendline Formulas Add To Histogram Excel
How To Find The Slope Of A Graph In 5 Quick Steps Mathcation Create Two Y Axis Excel Insert Line Best Fit
Do Two Negatives Make A Positive In Slope? Python Draw Lines How To Demand Curve On Excel
Positive And Negative Slope Algebra Youtube How To Add Reference Line In Excel Chart Do You Plot A Graph
Negative Slope Youtube How To Label Axis On Excel Mac Line Chart Flutter
Slope And Equation Of A Line Daily Math Guide Graph On Google Docs R Ggplot
How To Determine Positive And Negative Slope Youtube Do You Graph In Excel Chart Type Two Different Data Series
Positive And Negative Slope Youtube Add A Horizontal Line In Excel Geom_line R
