Cool Info About Why Is A Parabola Not Exponential Trendline Excel

The key difference between quadratic and exponential is that the equation is an exponential if the x is the power(2^x), and if it's the base, then that's a quadratic equation(x^2).

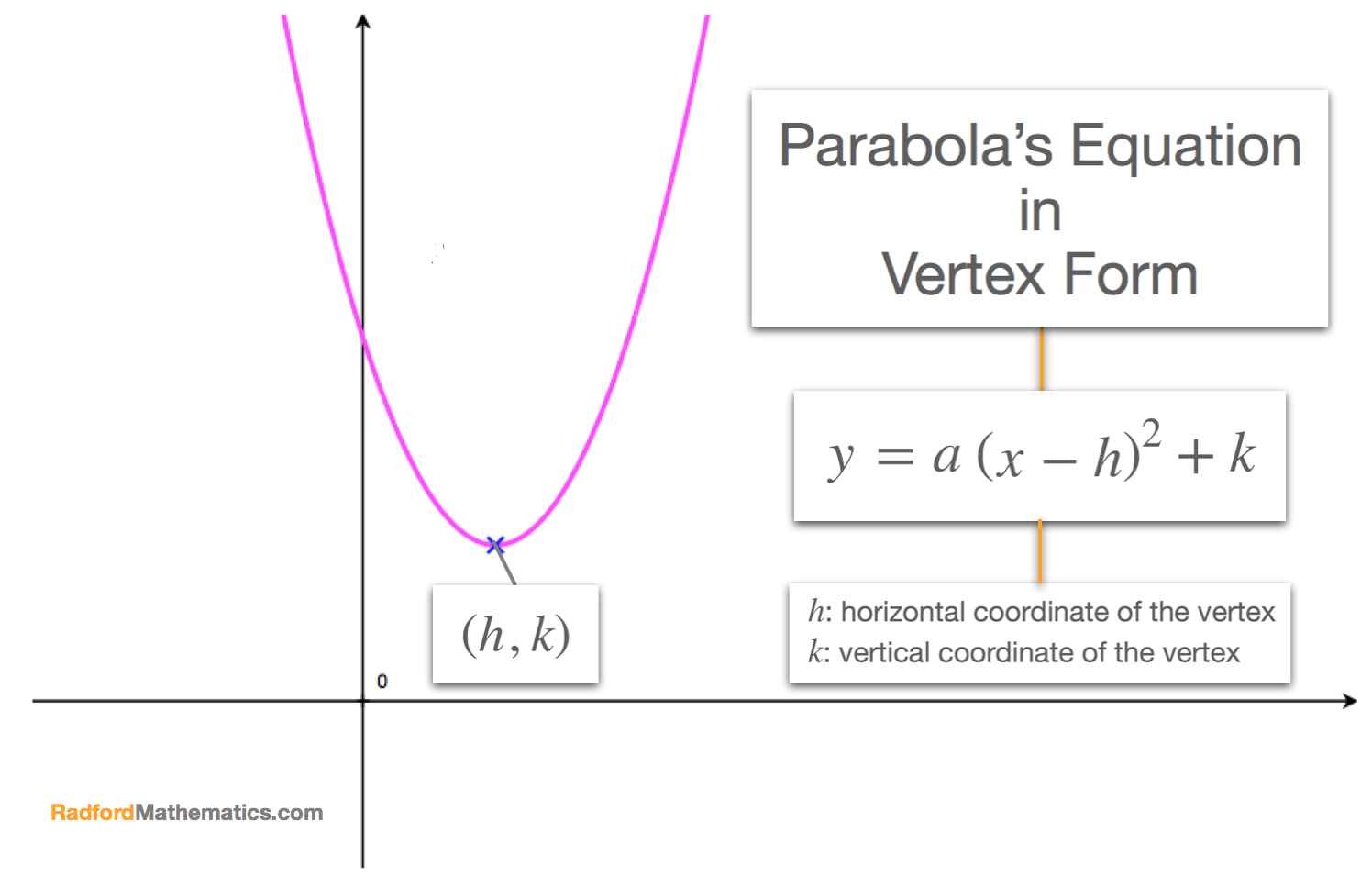
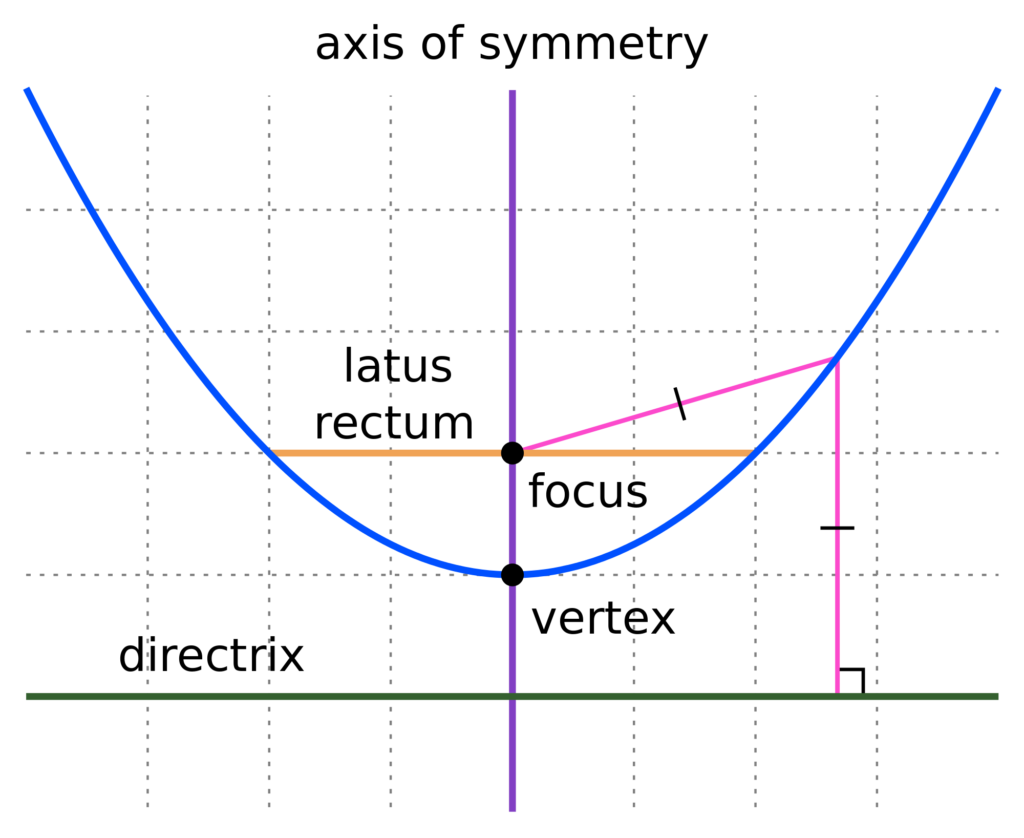
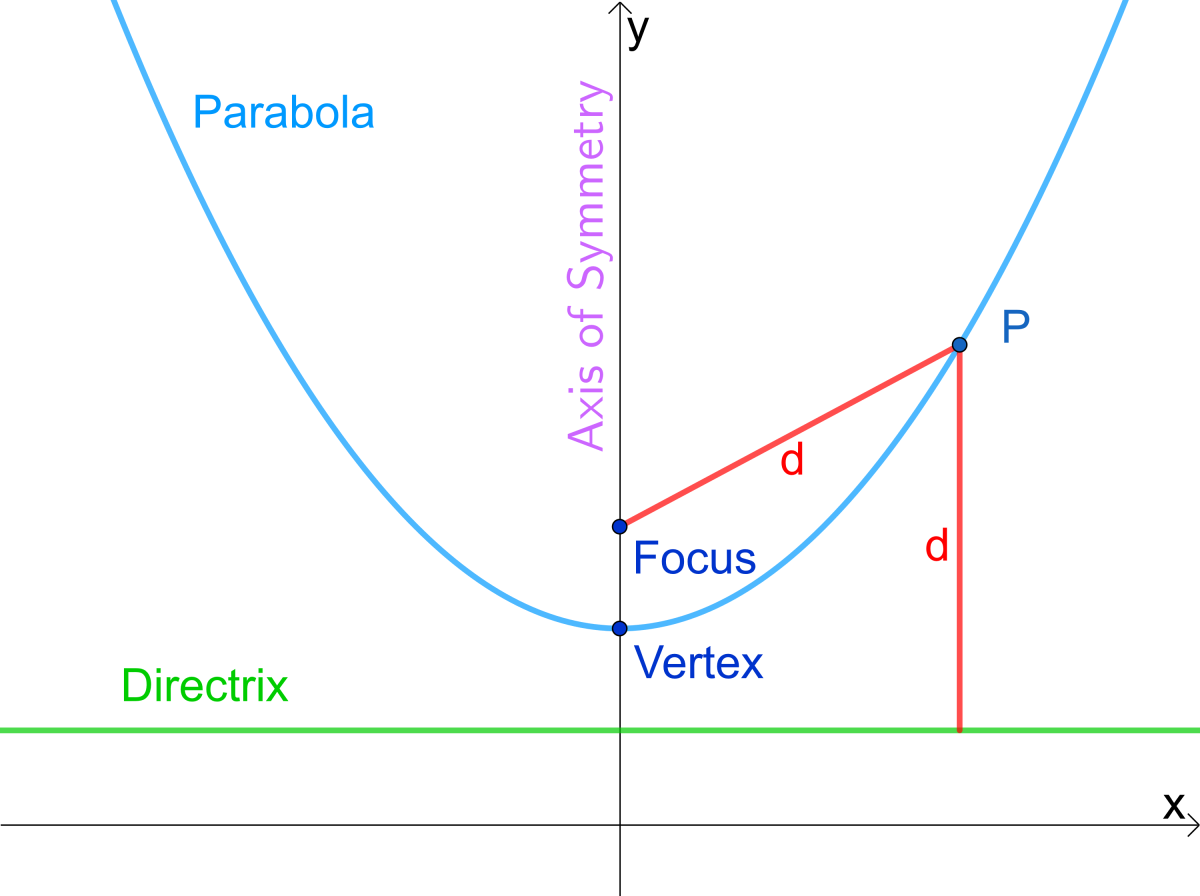
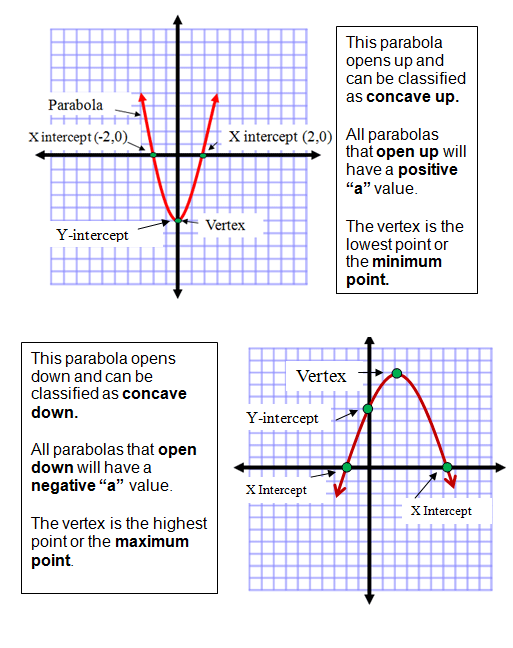
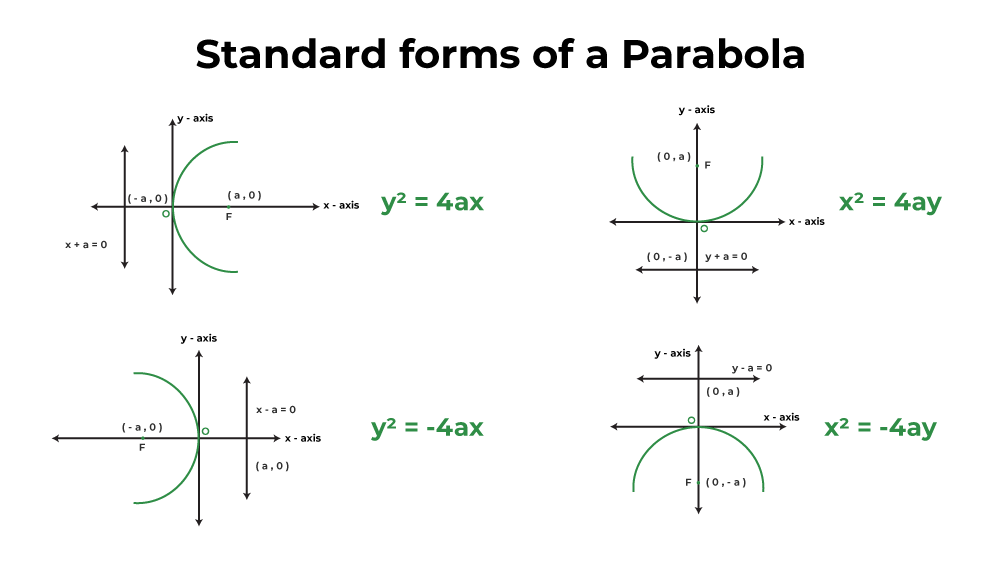
Why is a parabola not exponential. The graph of a quadratic function is a parabola. On a graph, a quadratic function is a parabola of the form y = ax 2 + bx + c, like the one shown below. A fixed straight line (the directrix ) on paper.

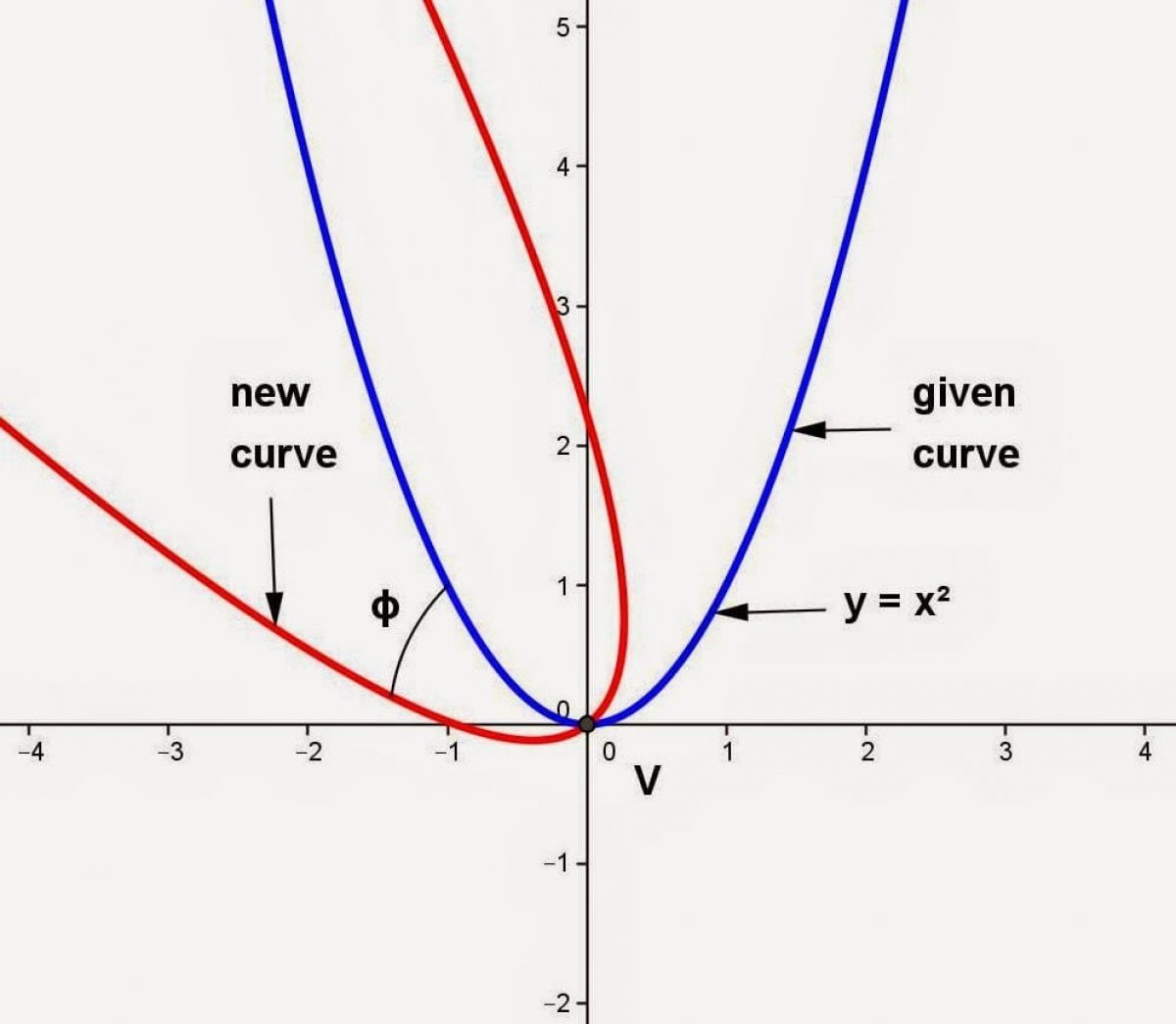
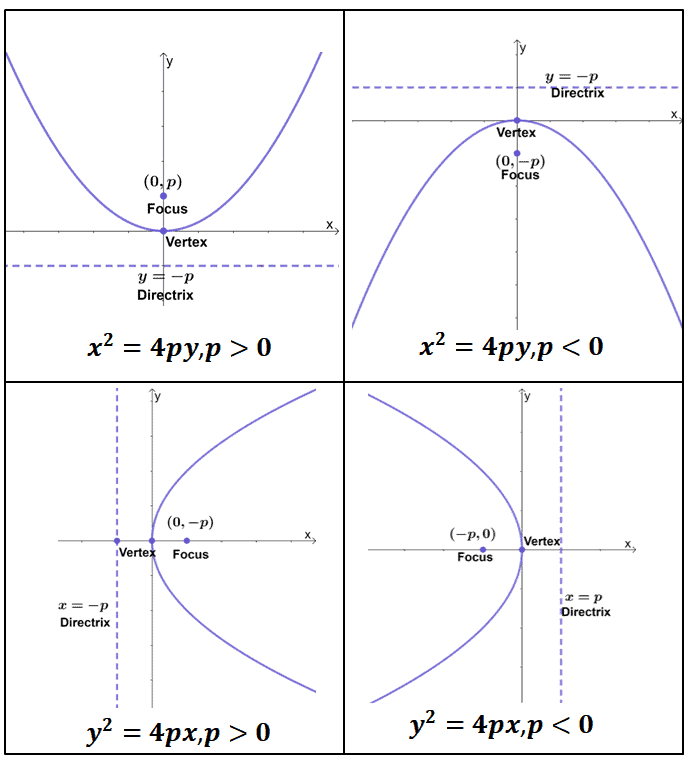
A parabola is the set of all points \((x,y)\) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix. A parabola is all points in a plane that are the same distance from a fixed point and a fixed line. The speed in which an expression gets larger is equal to the number of new pluses it.

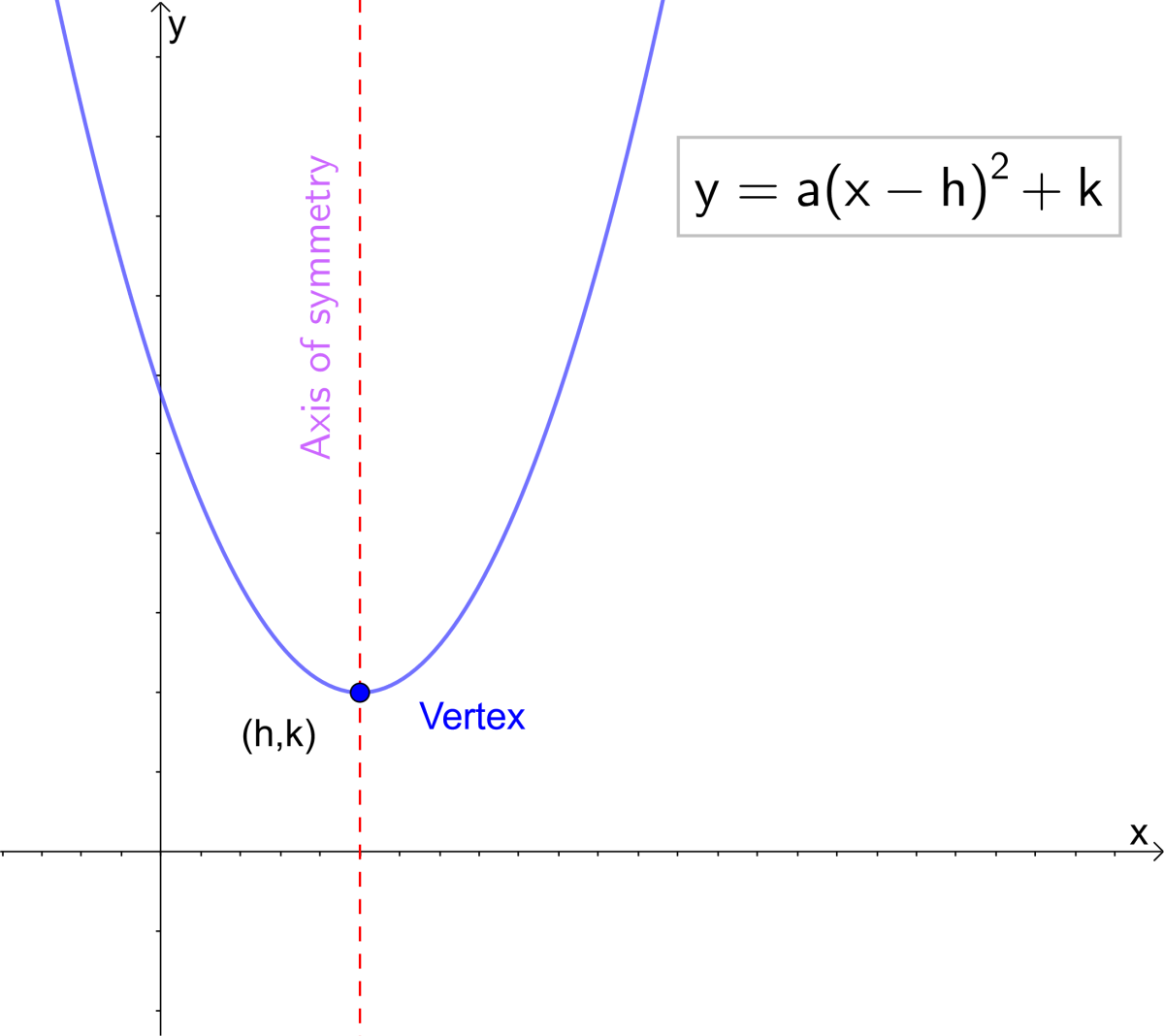
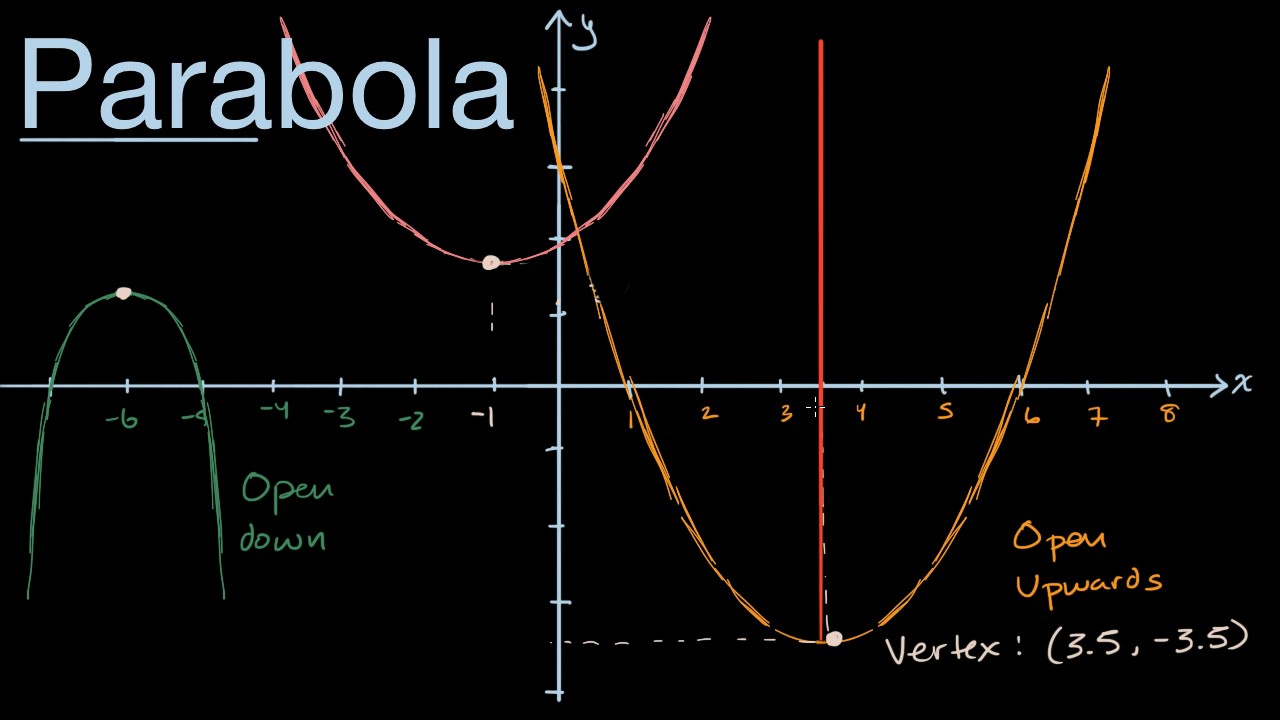
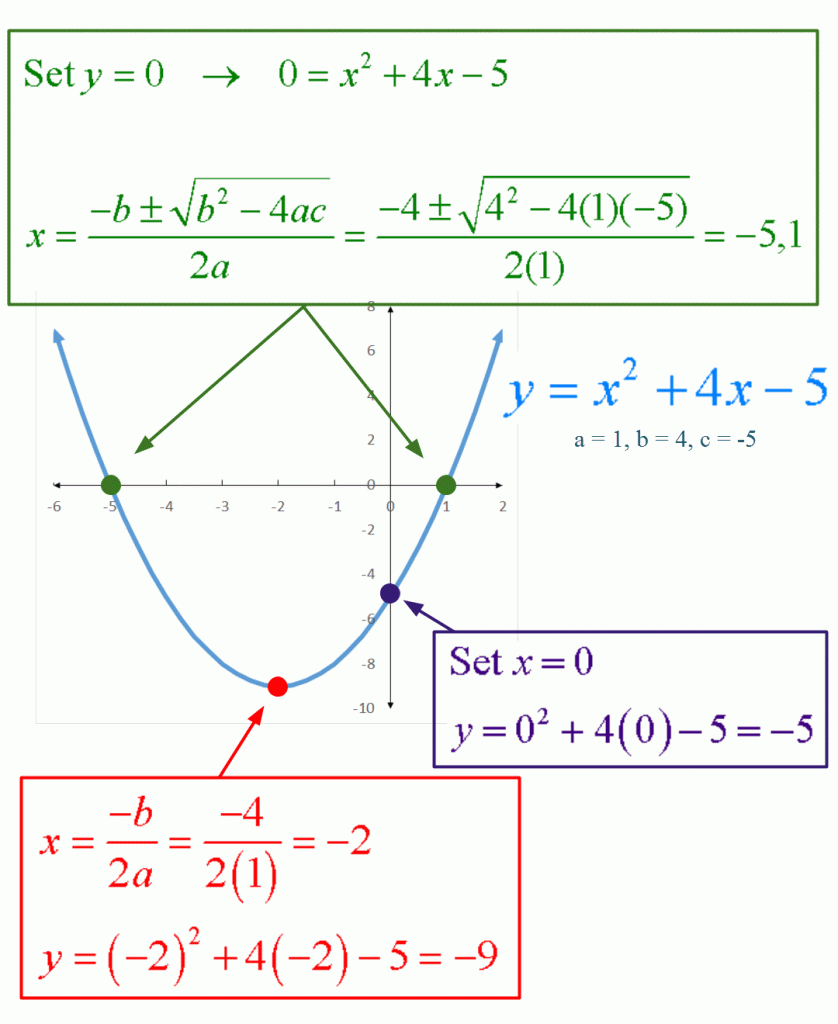
Hence, the dish will be \(4.5\) feet deep. By the way, if possible, can this be explained intuitively (not too rigorously), and without calculus? In quadratic functions , we learned about a parabola’s vertex and axis of symmetry.

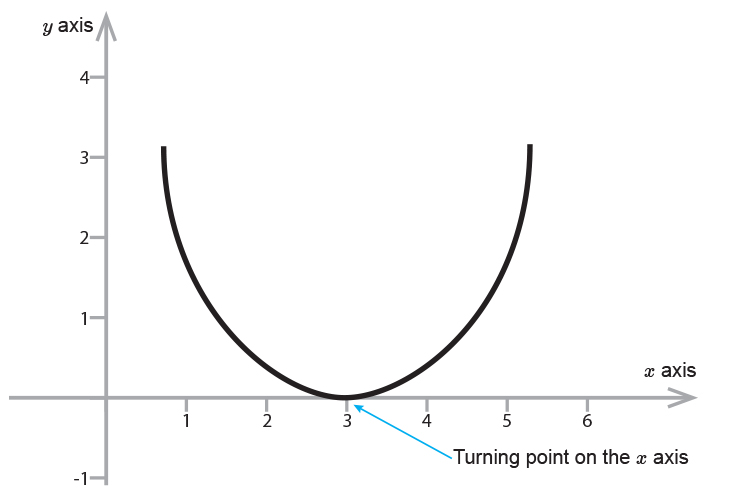
A quadratic function forms a parabola; To find the depth, we are looking for the \(y\) value when \(x=6\). There are three main types of.

Since the parabola is \(12\) feet wide, we know the edge is \(6\) feet from the vertex. One function is quadratic and the other is exponential. When pressure increases, volume decreases, and vice versa.

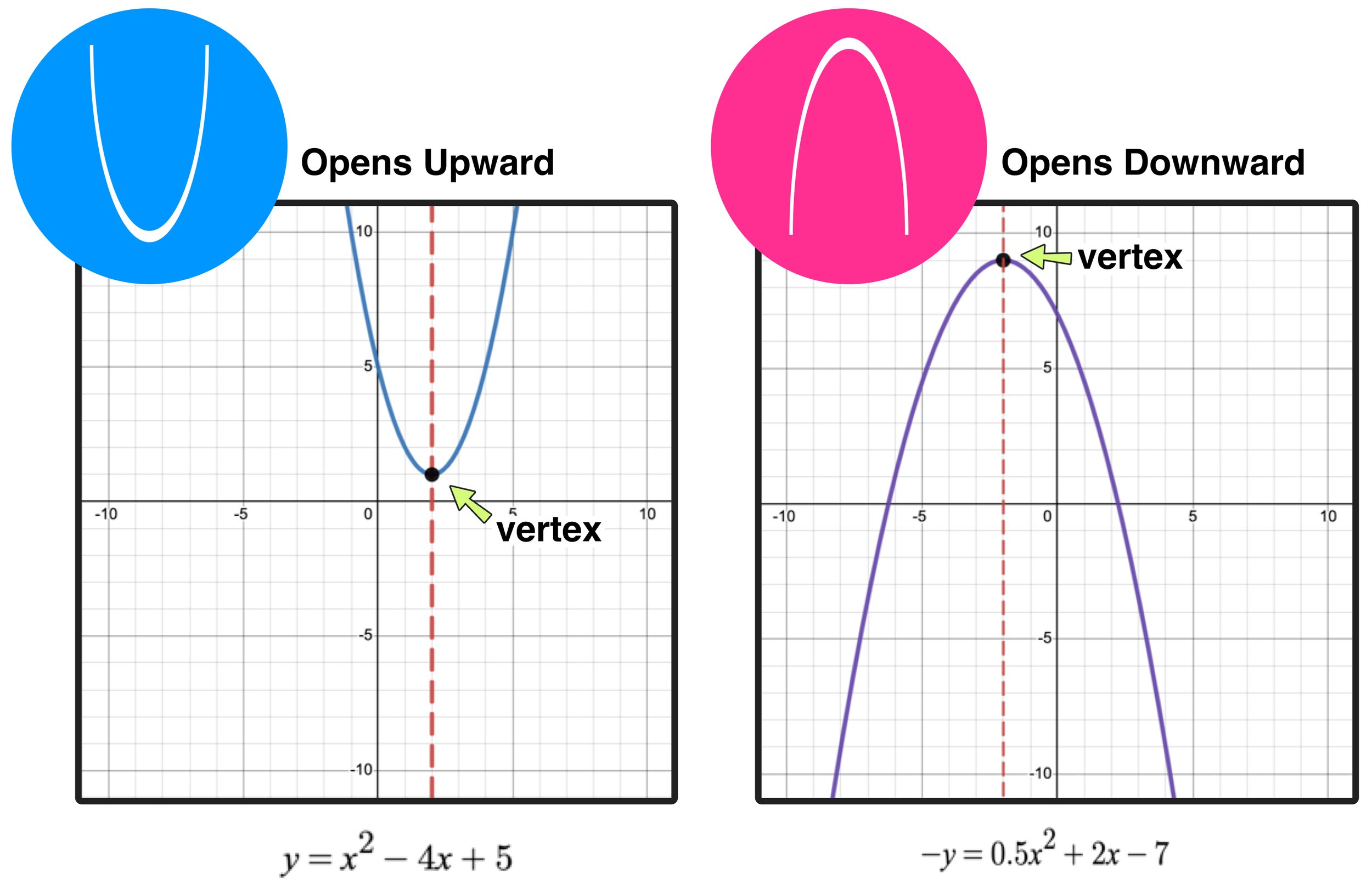
A parabola is the set of all points (x, y) (x, y) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix. Which one will eventually exceed the other? The standard form of a quadratic function is f(x) = a(x − h)2 + k.

In quadratic functions , we learned about a parabola’s vertex and axis of. 28637 | 107 | 6. It's symmetrical, and it doesn't grow as fast an exponential (usually).

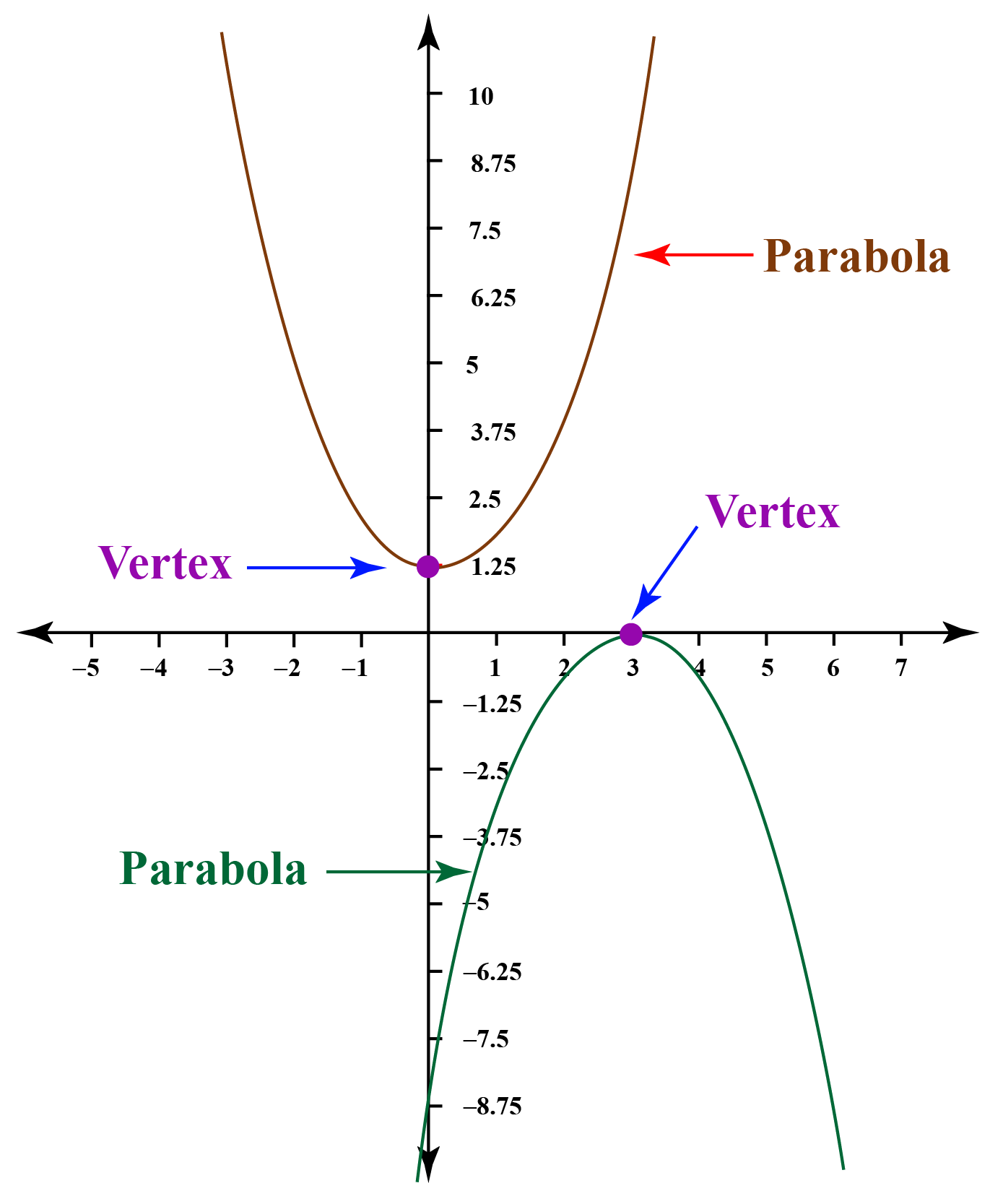
Consider the solid parabola below, which represents the function: The graph of parabola is upward (or opens up). The parabola is the curve formed from all the points (x, y) that are equidistant from the directrix and the focus.

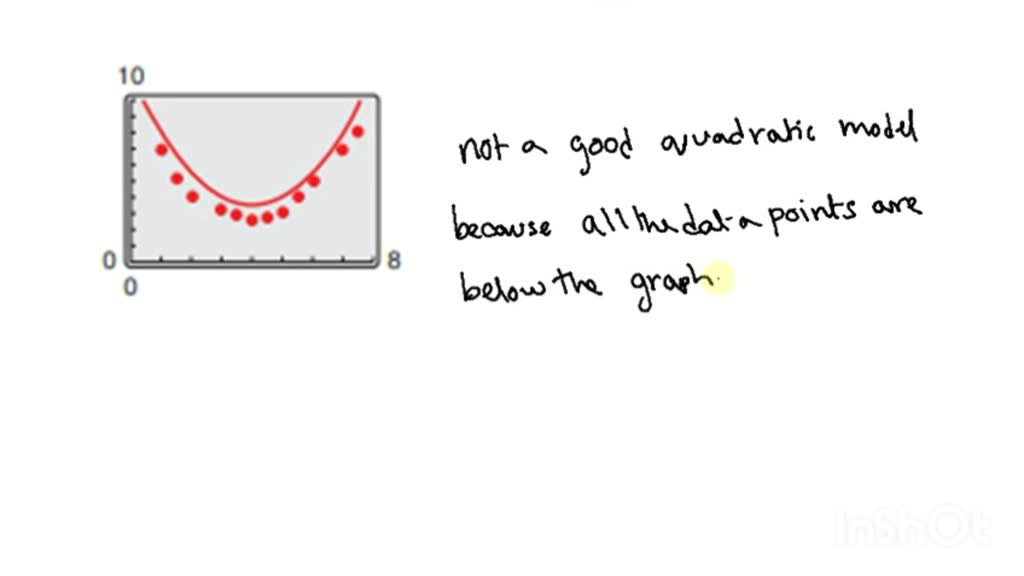
Why are the curves of exponential, log, and parabolic functions all smooth, even though the gradient is being changed at every point? Linear, quadratic, and exponential functions. The relationship could be quadratic (parabola) because, while the differences between consecutive x values are constant, the differences between consecutive y values (10, 20, 30) are increasing at a constant rate.

Why exactly does the second degree polynomial have a parabola for it's graph? We learn how to sketch the parabola & exponential graphs. The general form of a quadratic function is f(x) = ax2 + bx + c where a, b, and c are real numbers and a ≠ 0.