One Of The Best Tips About What Are The Conditions For A Smooth Curve Column Sparkline In Excel
Complex) solution than (0, 0, 0).
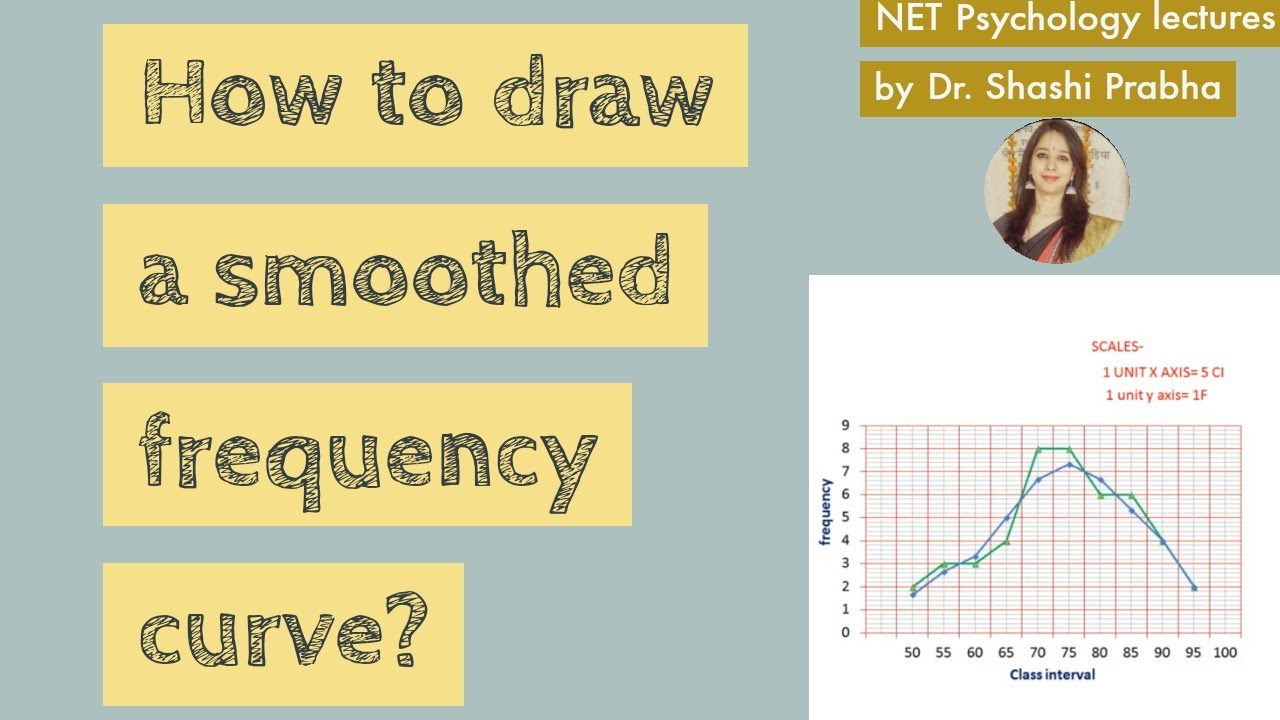
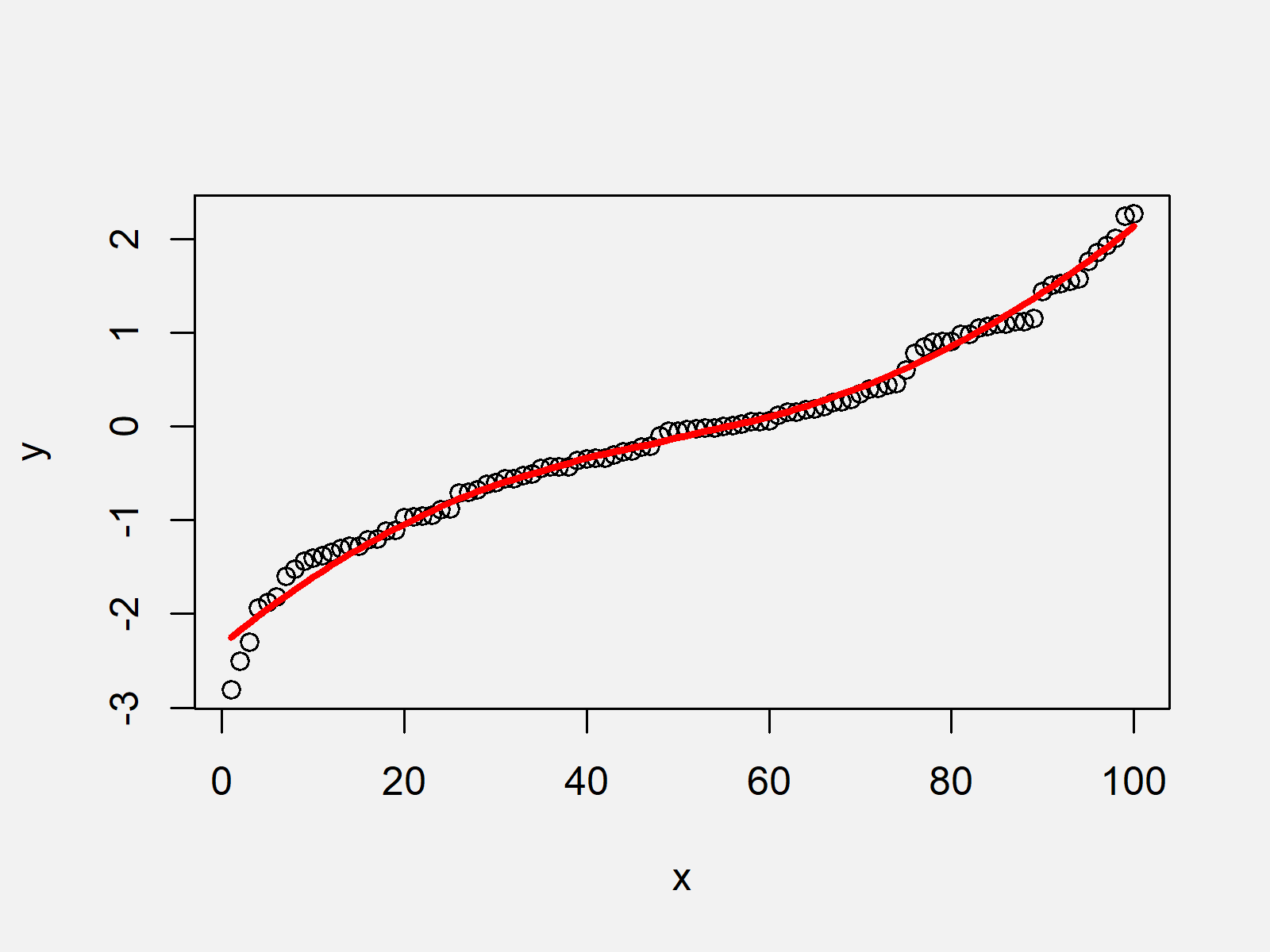
What are the conditions for a smooth curve. I → r3 is said to be regular if α'(t) ≠ 0 for all t ∊ i. When the test involved is a permutation test the number of possible permutations is limited and so the power curve has to have steps. We say that the curve $c$ is piecewise smooth curve when the two conditions below are satisfied:
Theorem is a powerful tool for classifying smooth projective curves, i.e. Complex) projective plane if the system has no other real (resp. \what are all the curves of a given genus (up to isomorphism)?
(i) $c \in c^{(0)}$ (ii) the domain over which the curve is defined can be partitioned into disjoint subsets such that the curve is in $c^{(\infty)}$ (or sufficiently. Giving us a start on the following questions: I → m be smooth curve.
There are some necessary conditions, involving good cohomology behavior. A unique normal vector to c at p. A point p of c is smooth if and only if there exists.
Suppose that given any open subset o of m containing γ[i], there exists a smooth symmetric field t ab on m such that: A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works. A smooth curve α:
In this question, for instance, a curve $\gamma \colon [a,b] \longrightarrow \mathbb{r^n}$ is defined to be smooth if all derivatives exist and are continuous. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context. Equivalently, we say that α is an immersion of i into r3.
We say that a smooth map (γ,ν):i → rn ×δn−1 is a framed curve if ˙γ(t)·νi(t) = 0 for all t ∈ i and i =1,.,n−1. A curve $\mathbf{r}(t)$ is considered to be smooth if its derivative, $\mathbf{r}'(t)$, is continuous and nonzero for all values of $t$. I → rn is a.
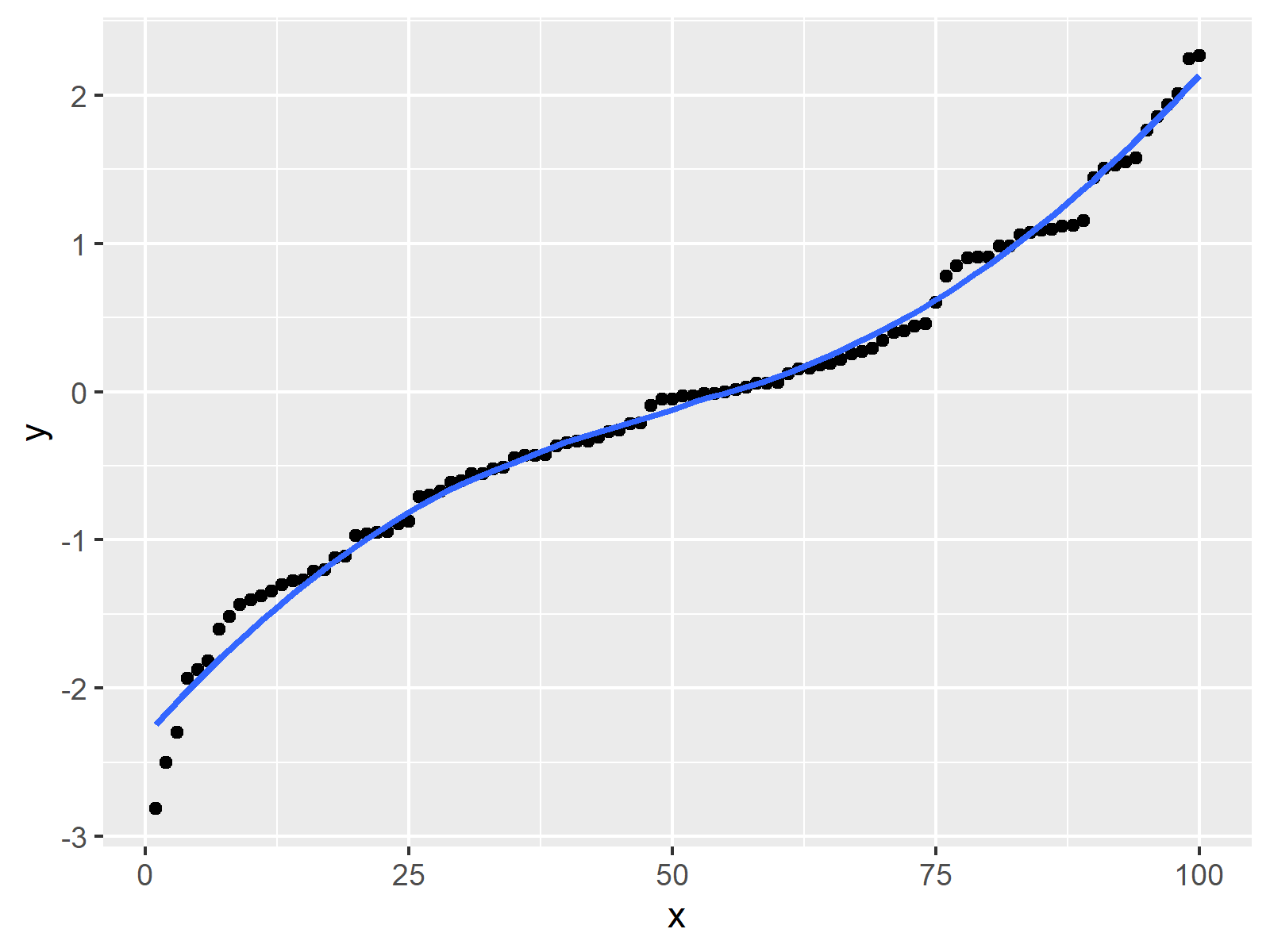
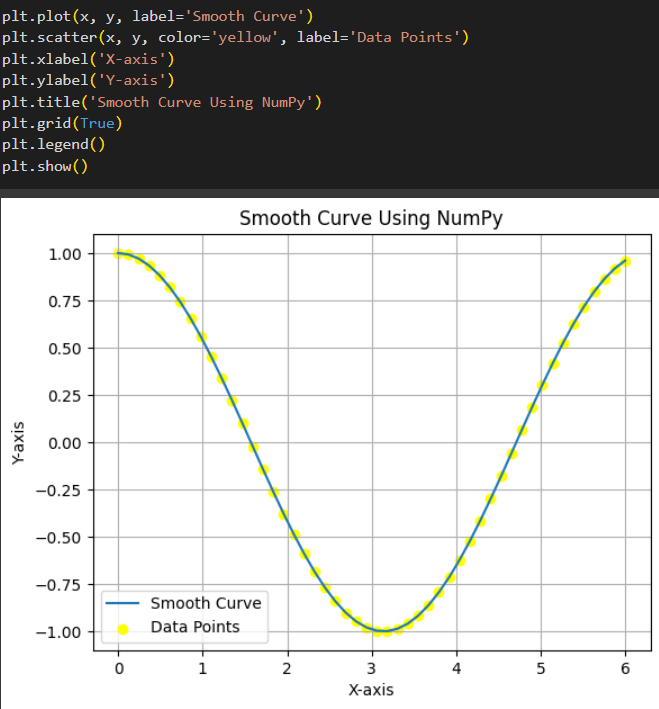
This task shows how to smooth a curve, i.e. $\begingroup$ usually when people say smooth, they mean 'continuously differentiable', but depending on the context higher order differentiability may be. The algorithm for identifying whether or not a parametric curve is smooth contains a first step of finding out when dx/dt and dy/dt is simultaneously 0.
(1) t ab satisfies the. We also say that a smooth map γ: If x is smooth and proper over the complex numbers, you get a variation of hodge structure.
Basic properties of such curves may be found in [1]. In particular, a smooth curve is a. A simple closed curve is a curve $c$ that has a parametrization $\bfx = \bfg(t)$, $a\le t \le b$ (with $a<b$) such that $\bfg$ is continuous and $\bfg(a) = \bfg(b)$.


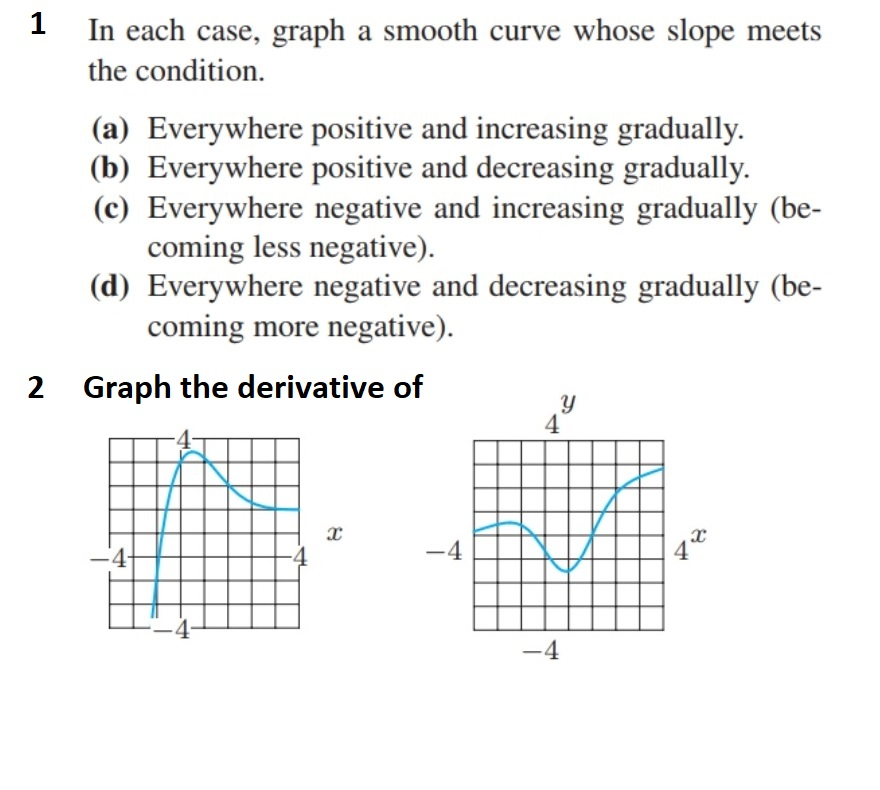


![[2 marks] 9. The curve shown below is a smooth curve.](https://media.cheggcdn.com/study/beb/beb99b3a-ee88-4088-9067-d95c83fdb34f/image)