Smart Tips About What Does R2 Tell Us About The Best Fit Line Power Bi Dual Axis Chart
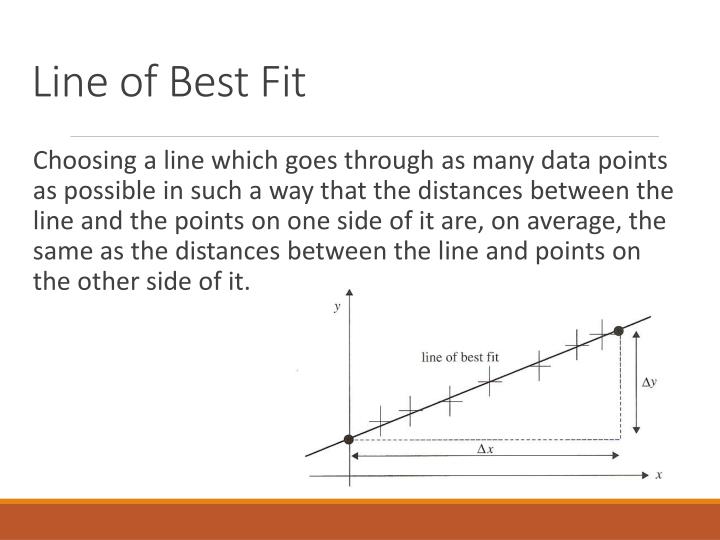
For example, the graphs below show two sets of simulated data:
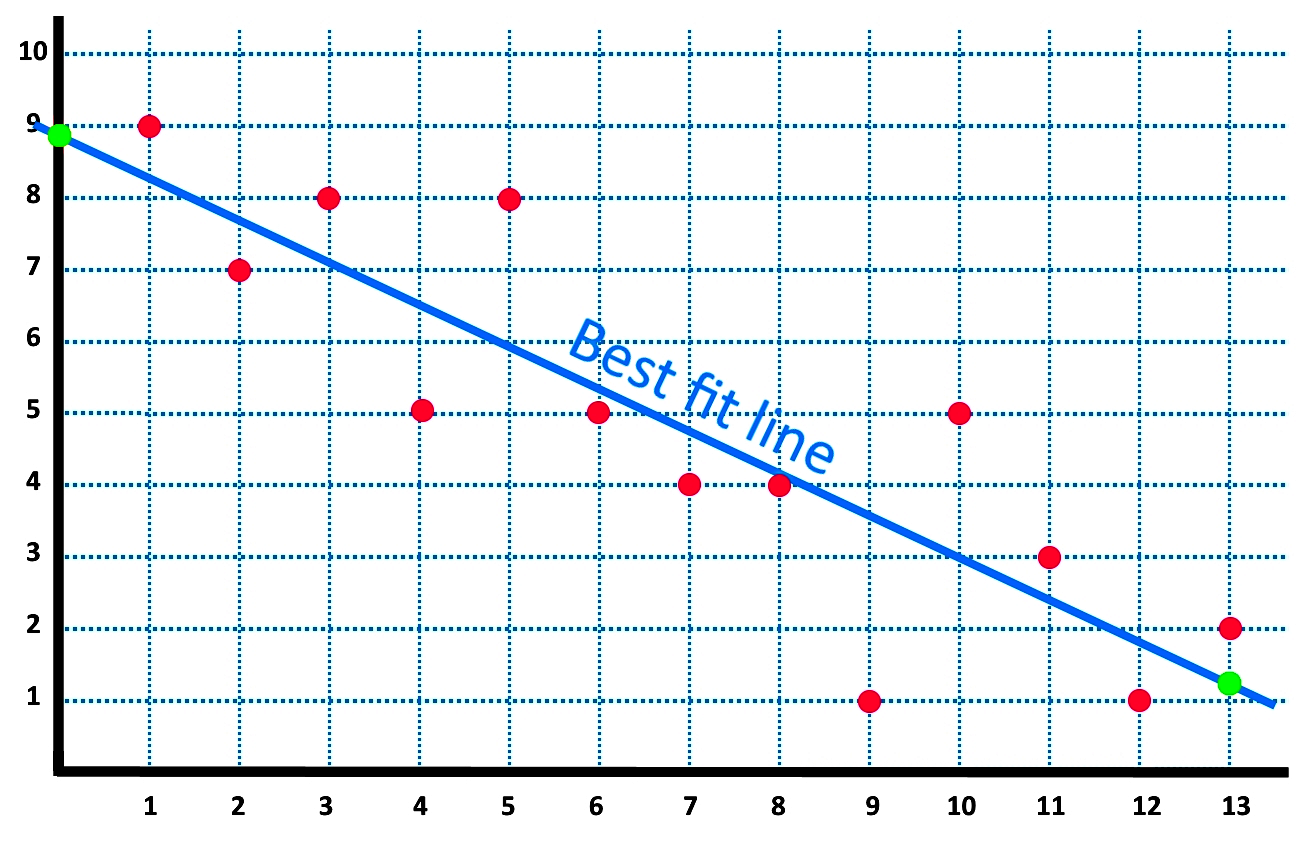
What does r2 tell us about the best fit line. The observations are shown as dots. It is an output of regression analysis and can be used as a. Graphing your linear regression data usually gives you a good clue as to whether its r 2 is high or low.
This statistic indicates the percentage of the variance in the dependent variable that the. Sey is the total variation in y (sum of squared distances from the mean of y) and tells you the how much the data deviates from the mean of y. The criteria for the best fit line is that the sum of.
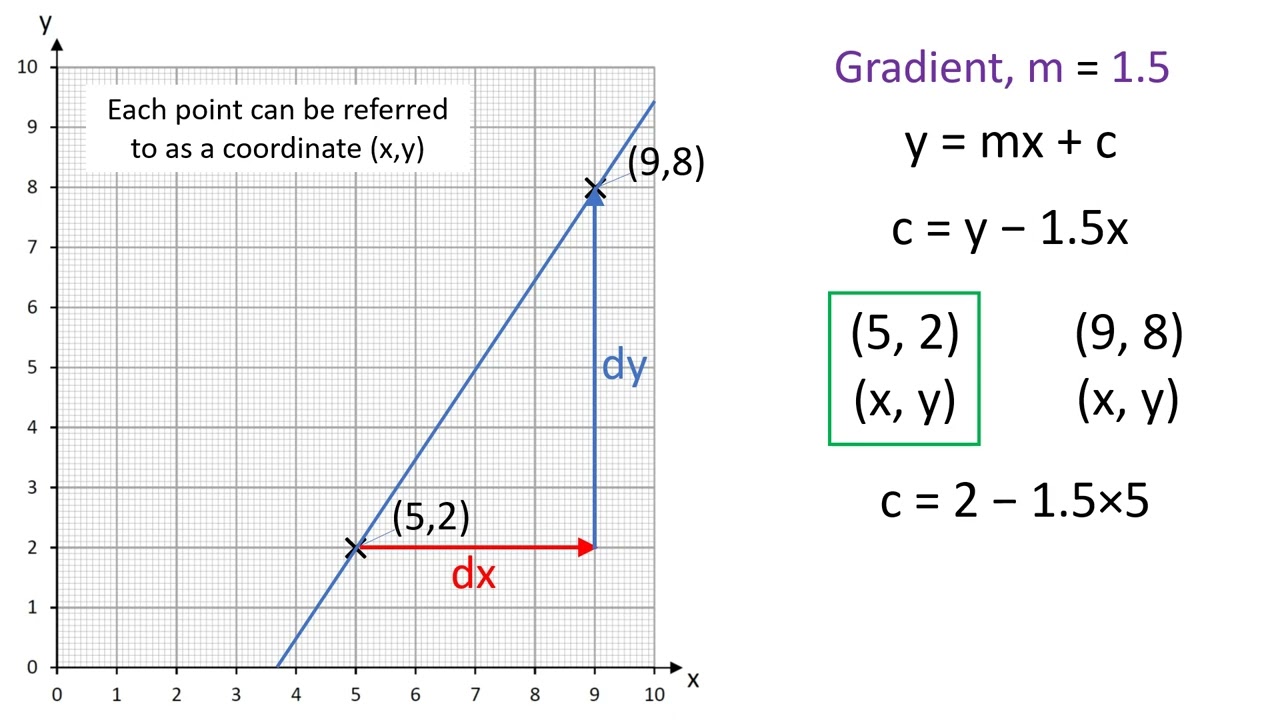
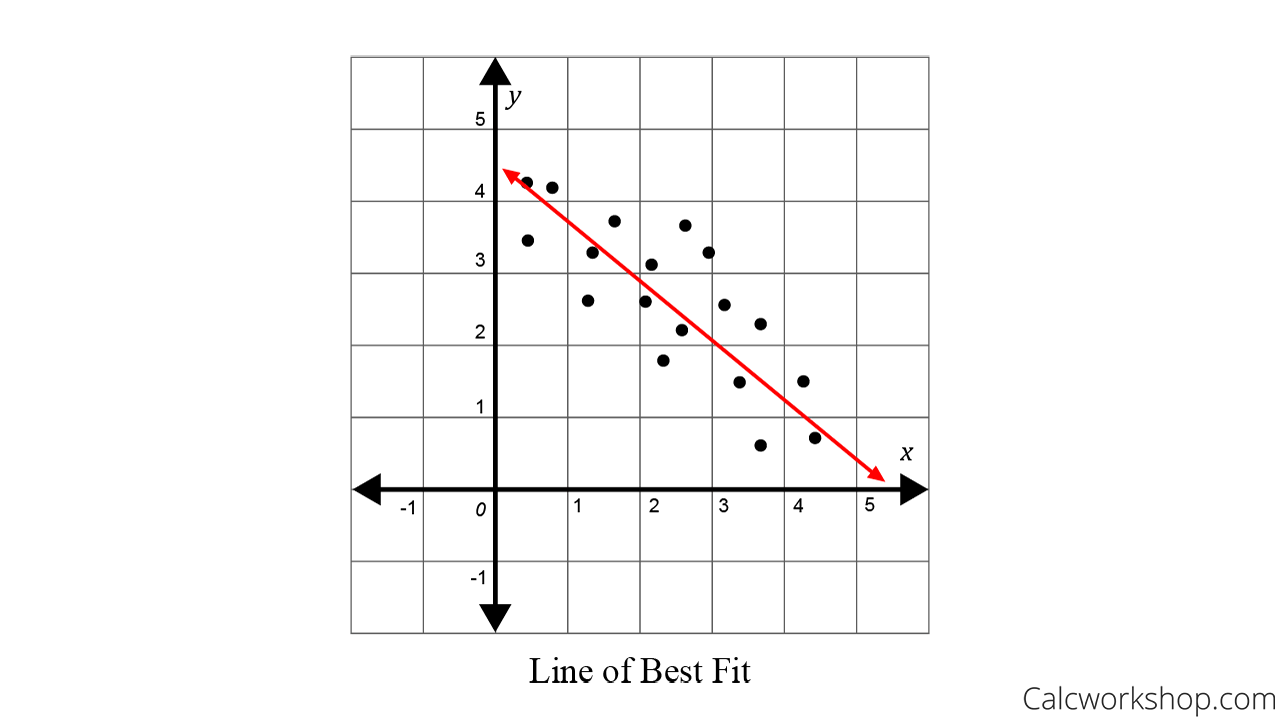
R² = 1 implies that the regression line is a perfect fit. The line of best fit is used to express a relationship in a scatter plot of different data points. The value r2 is a fraction between 0.0 and 1.0, and has no units.
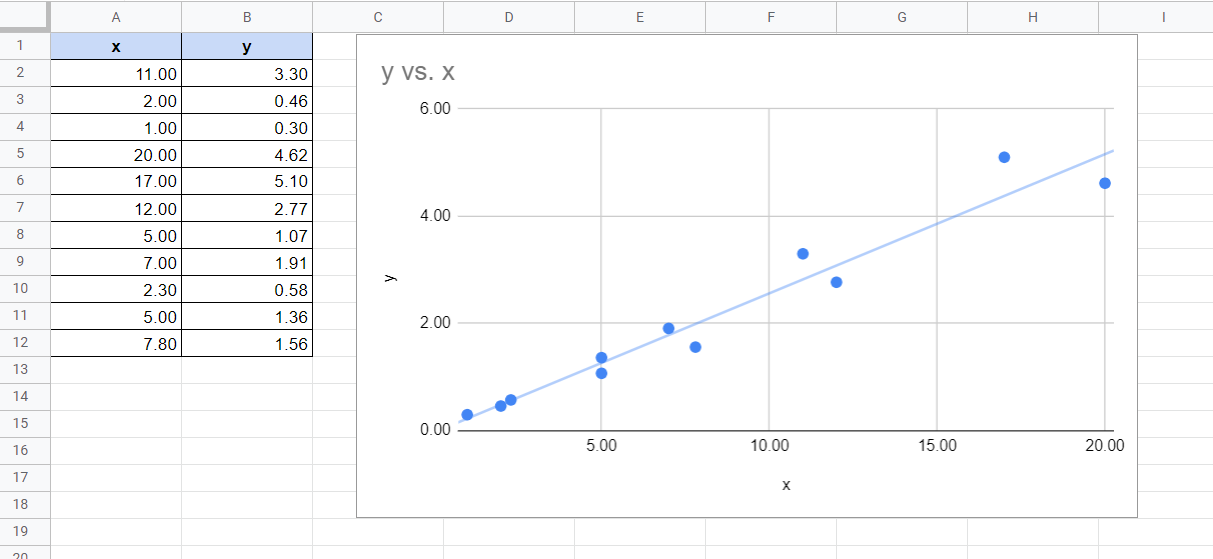
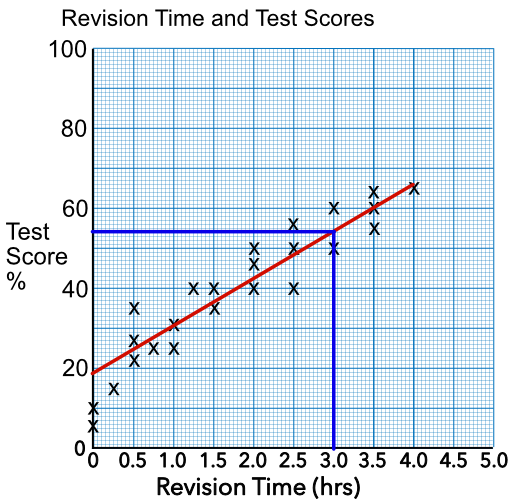
The better the linear regression (on the right) fits the data in comparison to the simple average (on the left graph), the closer the value of r2 is to 1. One of the most important metrics when. First, you use the line of best fit equation to predict y values on the chart based on the corresponding x values.
The model’s predictions (the line of best fit) are shown as a black line. First recall that the linear best fit line is the line which minimizes the sum of squared residuals (see least squares): $$\sum_{i=1}^{n}{r_i^2}$$ where $r_i$ is the residual for.
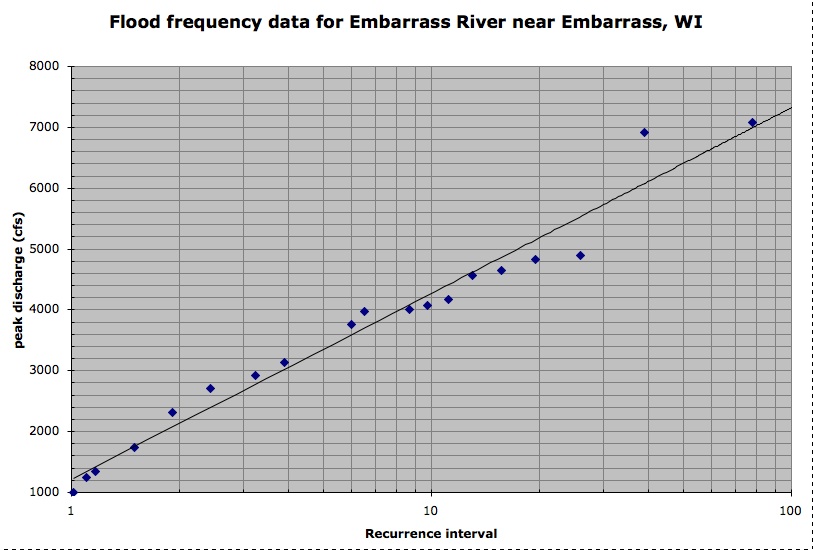
As a result, r 2 is also called the coefficient of determination. Statistics and probability questions and answers. The fitted line plot displays the relationship between semiconductor electron mobility and the natural log of the density for real experimental data.
An r2 value of 0.0 means that knowing x does not help you predict y. Choose the correct answer below. The variation in y gives you a baseline by which to judge how much better the best fit line fits the data.
What does an r squared value. Once the line of best fit is in place, analysts can create an. Brooke franklin and jason segall.
There is no linear relationship between x. R² = 0 implies that the regression line does not fit the data at all. It is best defined as the percentage of variation in the dependent or predicted variable (y) that can be.


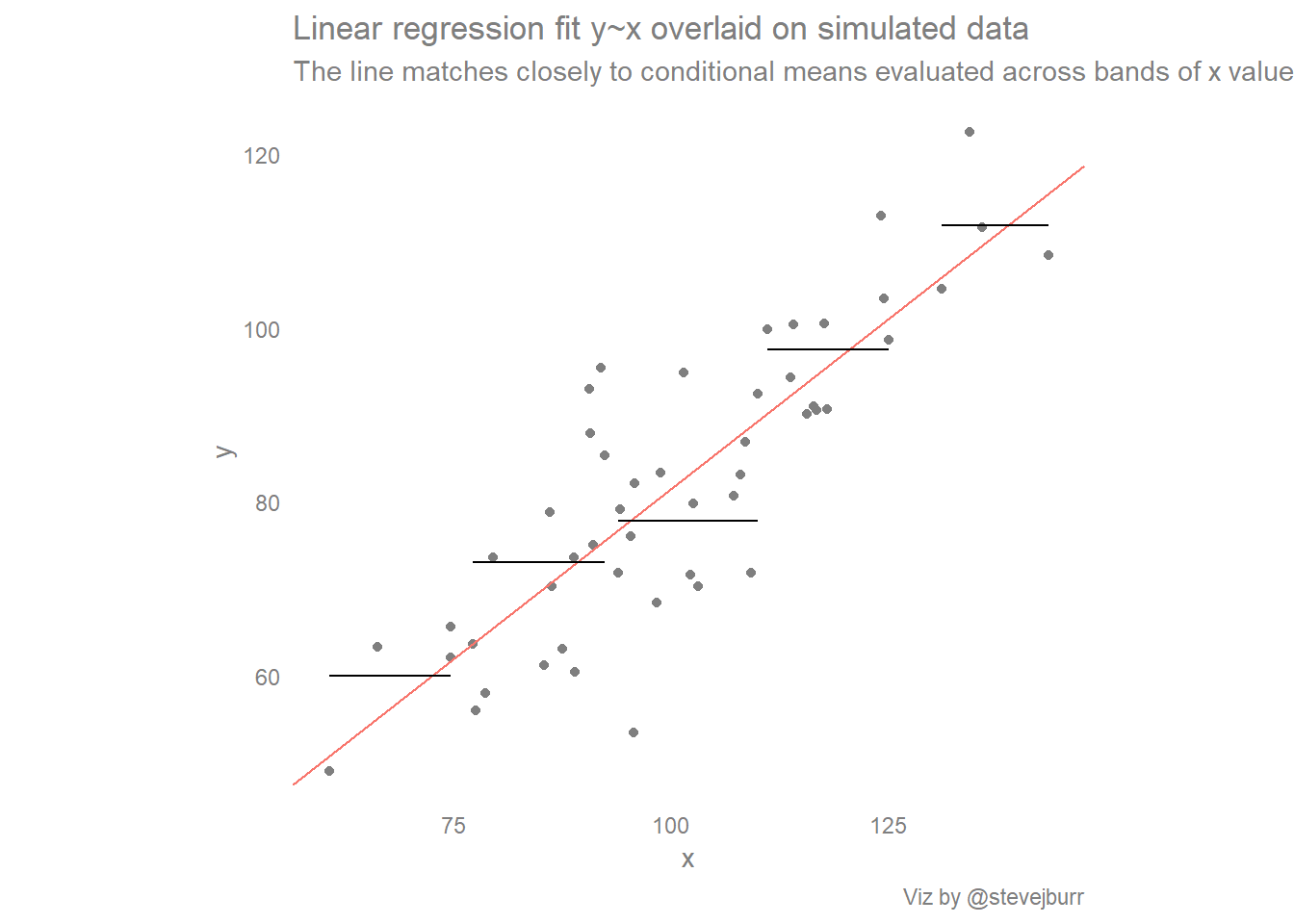



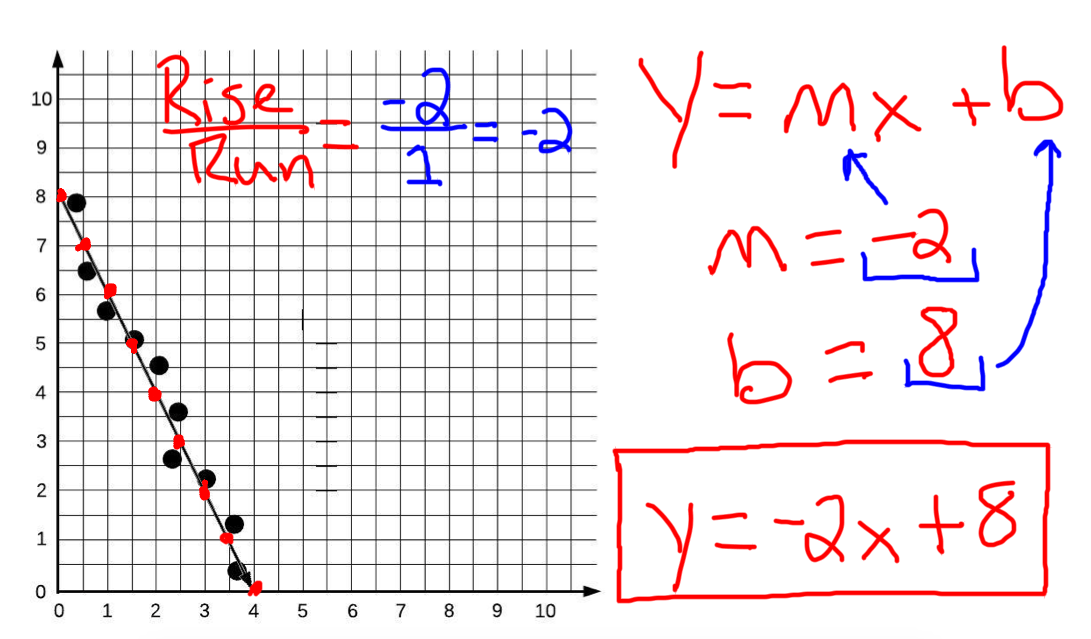

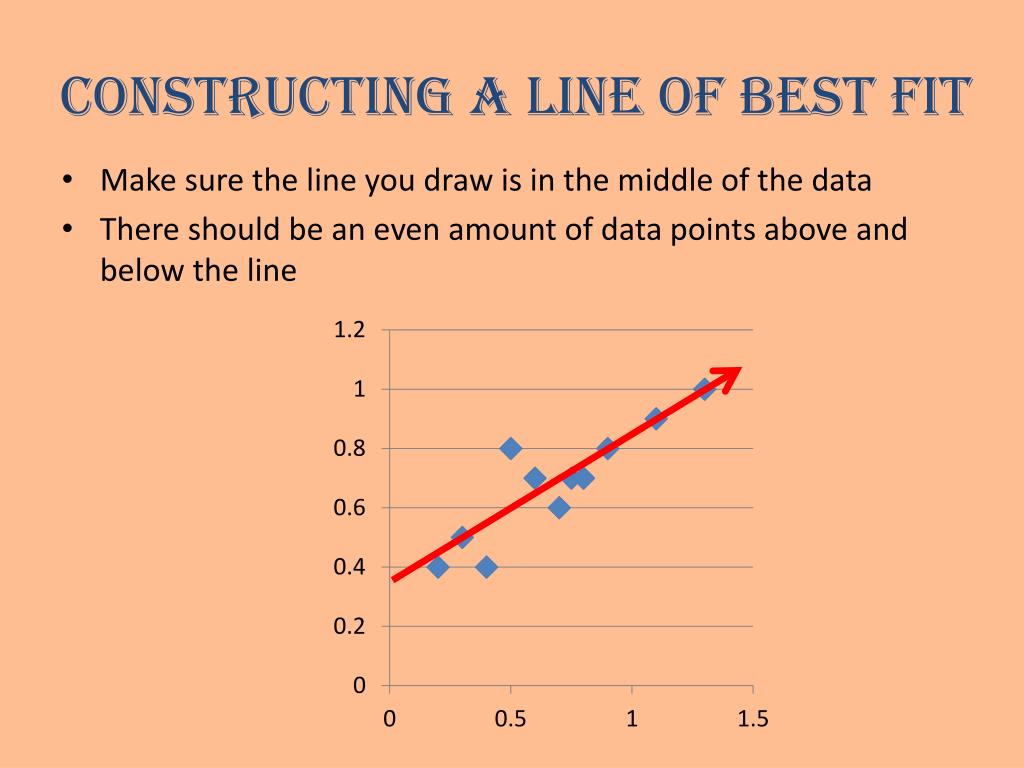



:max_bytes(150000):strip_icc()/Linalg_line_of_best_fit_running-15836f5df0894bdb987794cea87ee5f7.png)