First Class Tips About How To Interpret The Slope Of Line Fit Vertical Matlab

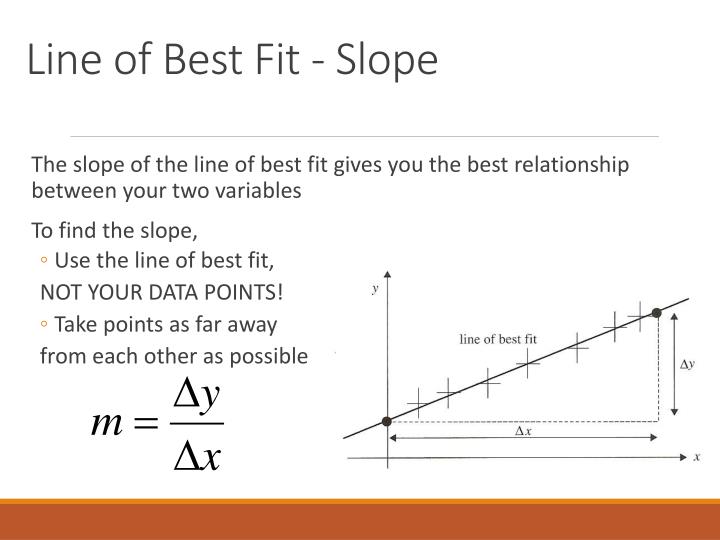
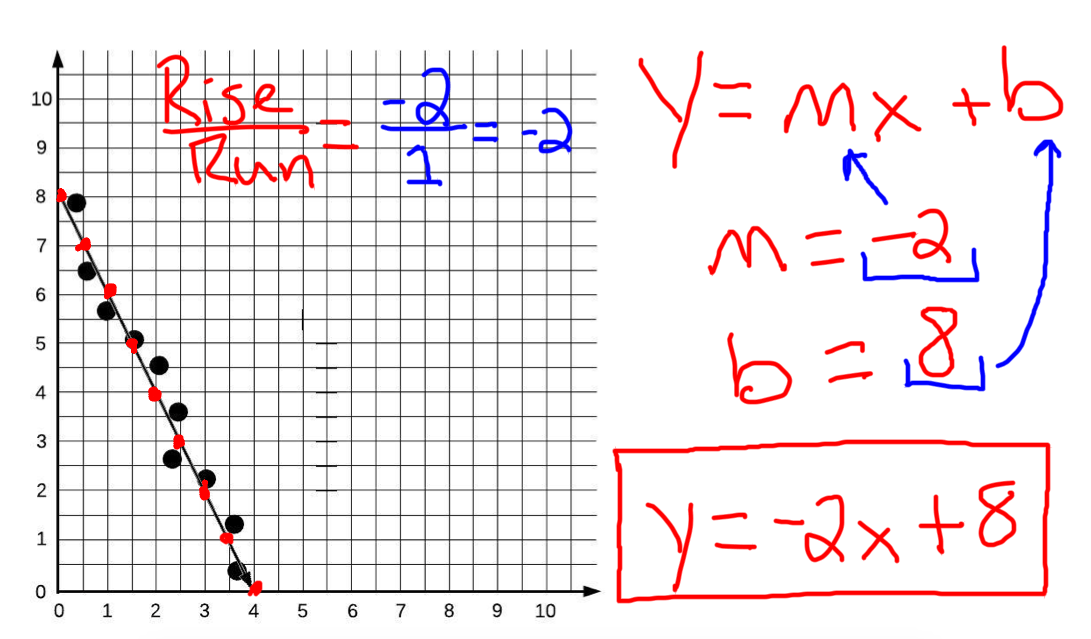
M is the slope or the consistent change.

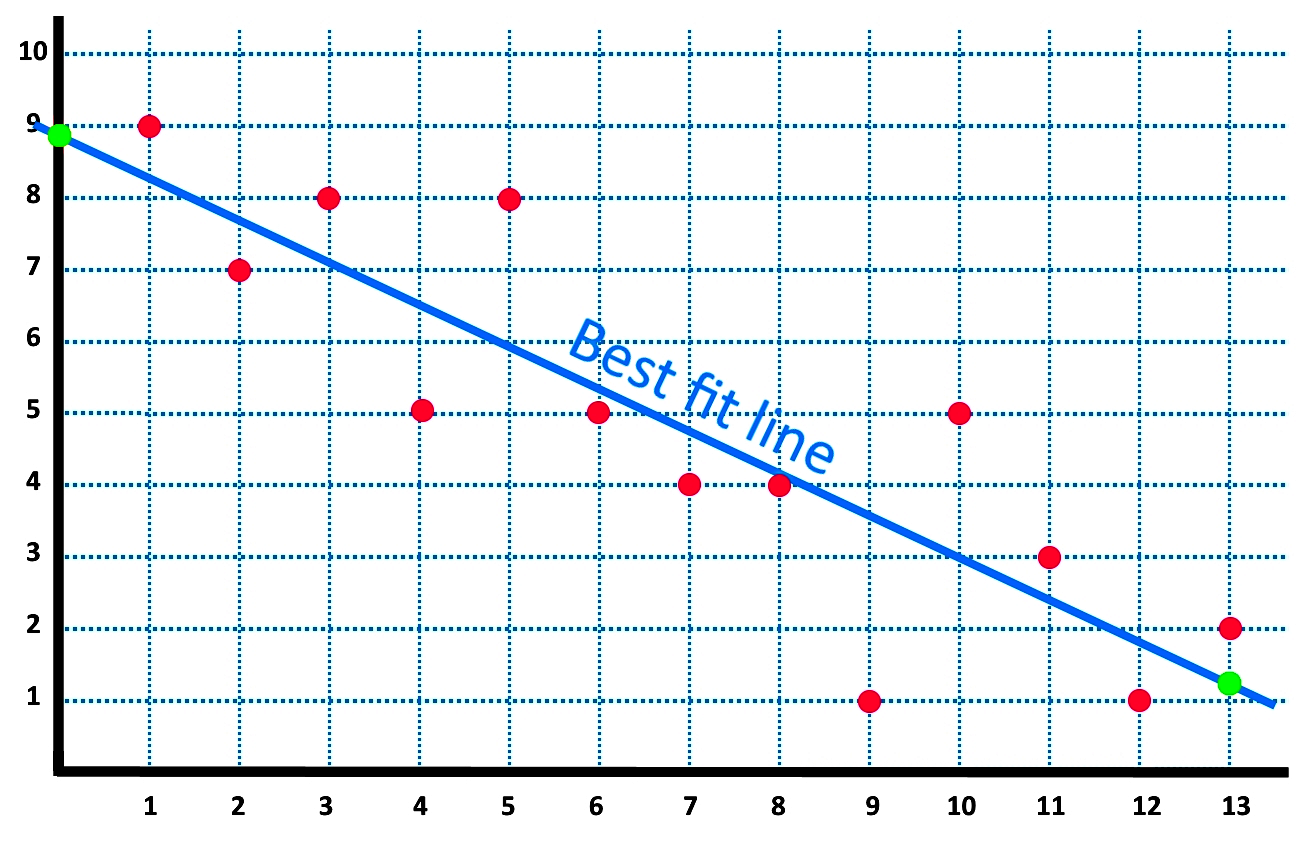
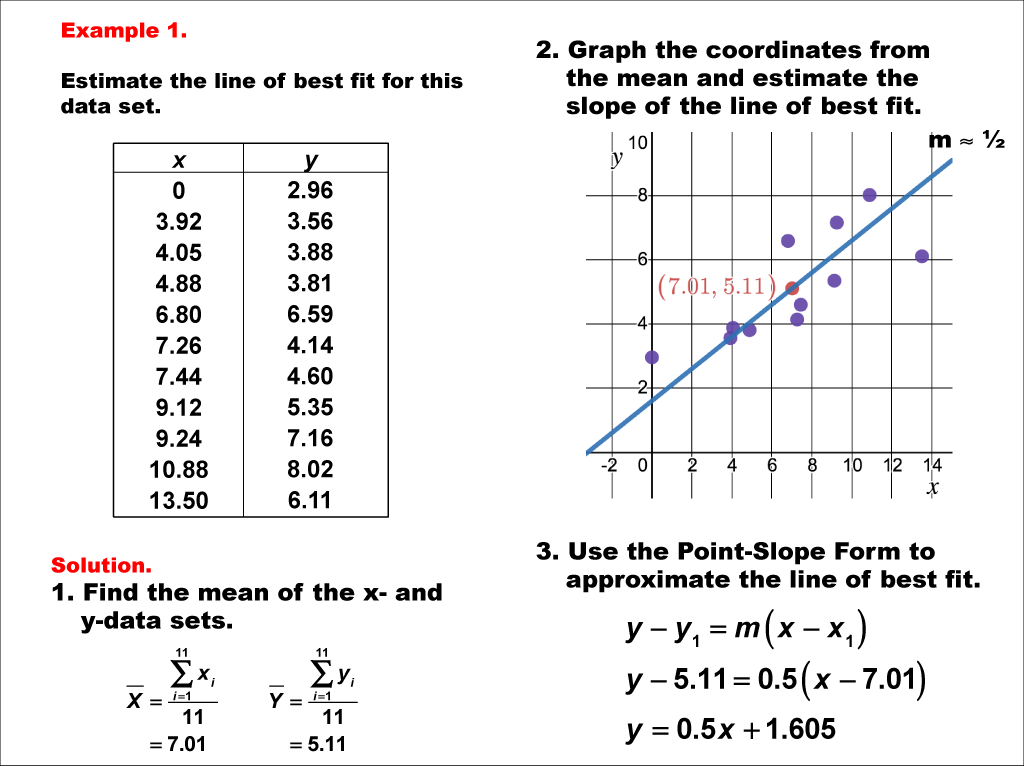
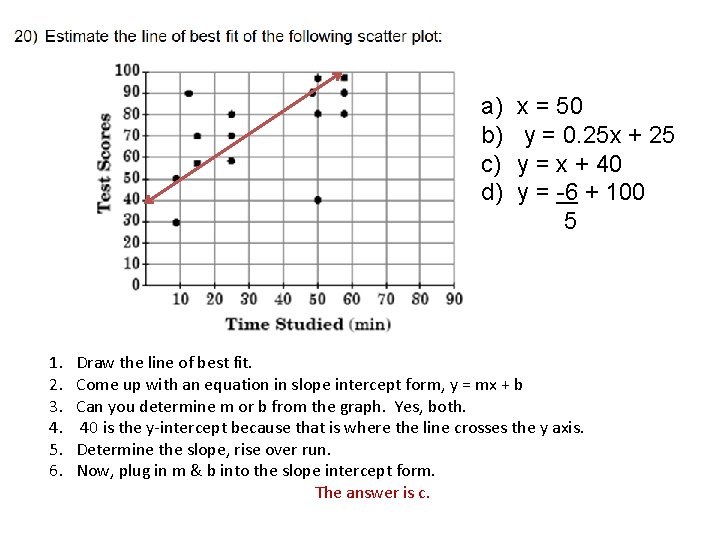
How to interpret the slope of the line of fit. One way to approximate our linear function is to sketch the line that seems to best fit the data. You can find the equation for the line of best fit using the least square method in four steps. Eyeball method, point slope formula, or least square method.

How can i fix this kind of problem? We interpret scatter plots, investigate the relationship between variables, interpret the slope of a trend line, and make predictions. A panel of judges was asked to judge the quality of different kinds of potato chips.

The line of best fit is calculated using the least squares method, which minimizes the sum of the squares of the vertical distances between the observed data points and the line. Instead, the idea is to get a line that has equal numbers of points on either side. See examples of making predictions from it.

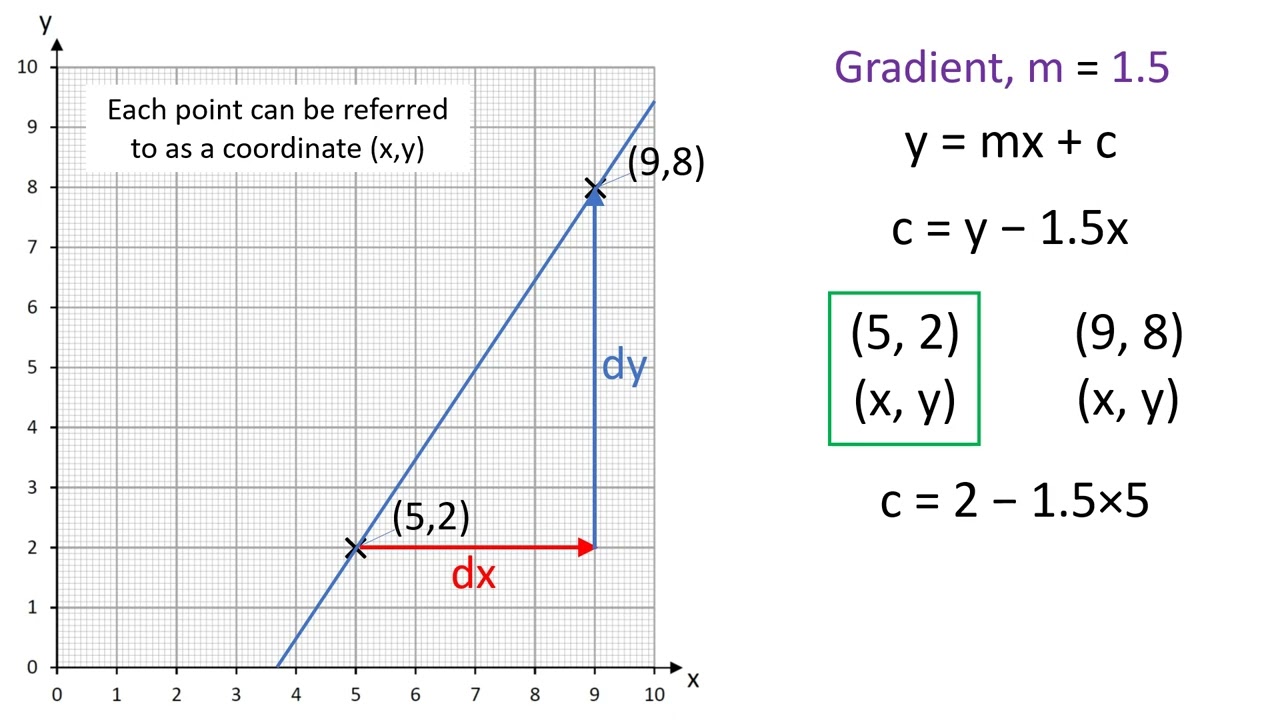
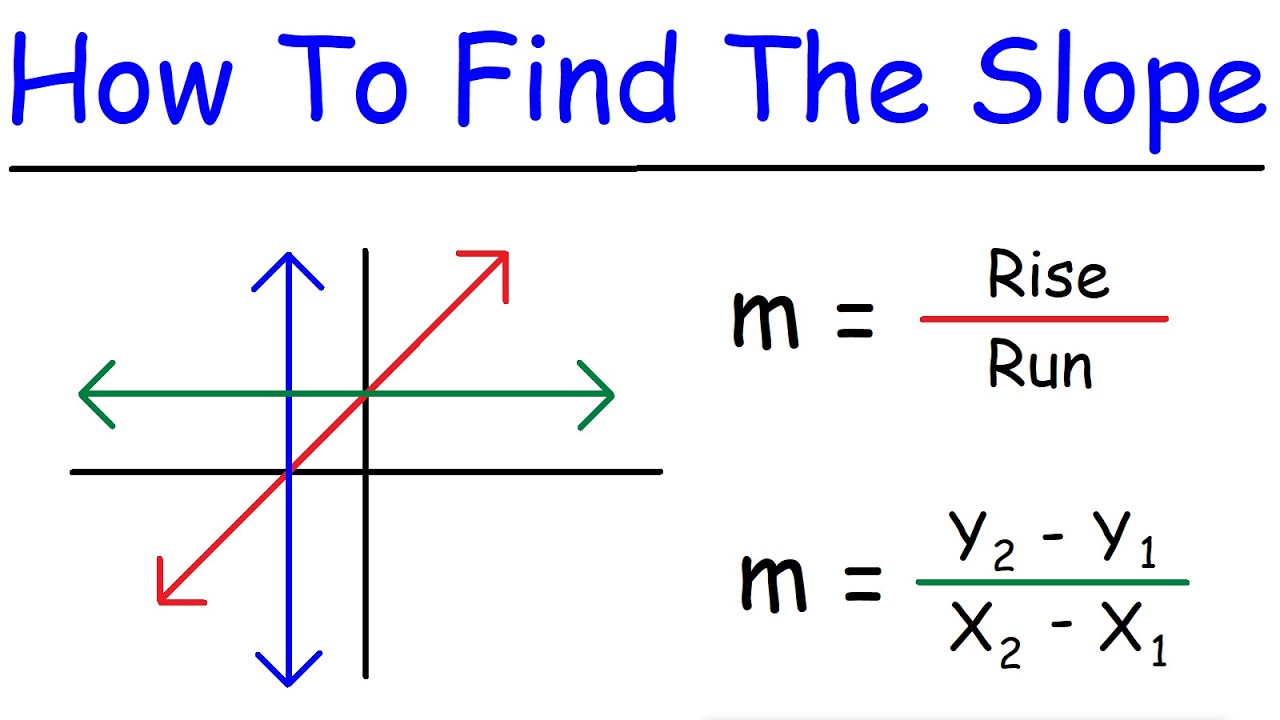
The slope (m) can be calculated by finding the change in y divided by the change in x between two points on the line. In many cases, the line may not pass through very many of the plotted points. A common issue when we learn about the equation of a line in algebra is to state the slope as a number, but have no idea what it represents in the real world.

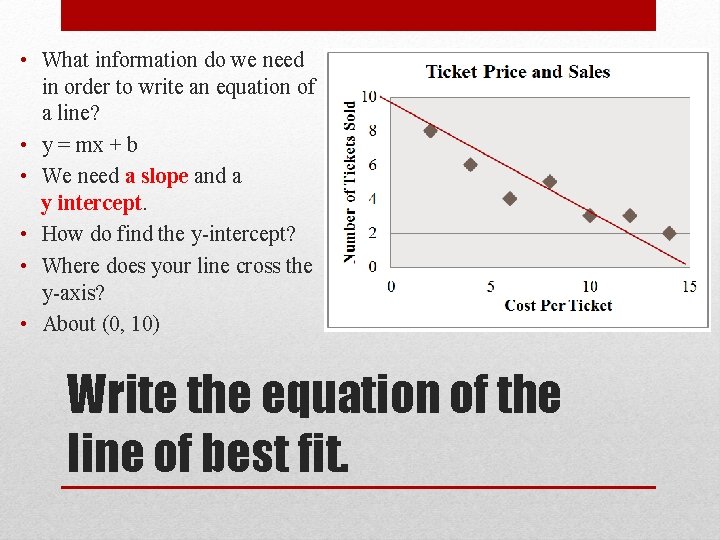
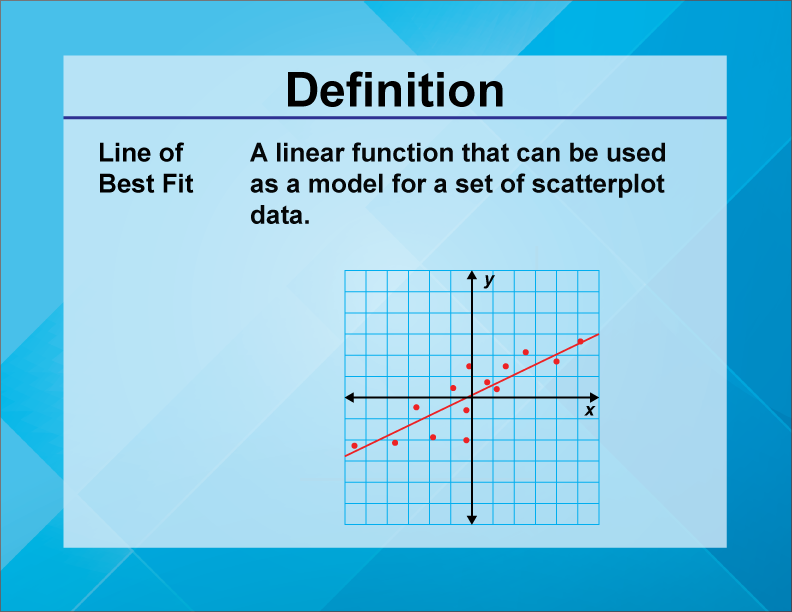
The equation of the line of best fit is y = ax + b. The 'line of best fit' is a line that goes roughly through the middle of all the scatter points on a graph. The formula for the equation of the line of best fit is:

We show you how to draw a line of best fit by eye on a scatterplot and work out the equation of that line. Does line of best fit have to be exact? The least square method is the most accurate.

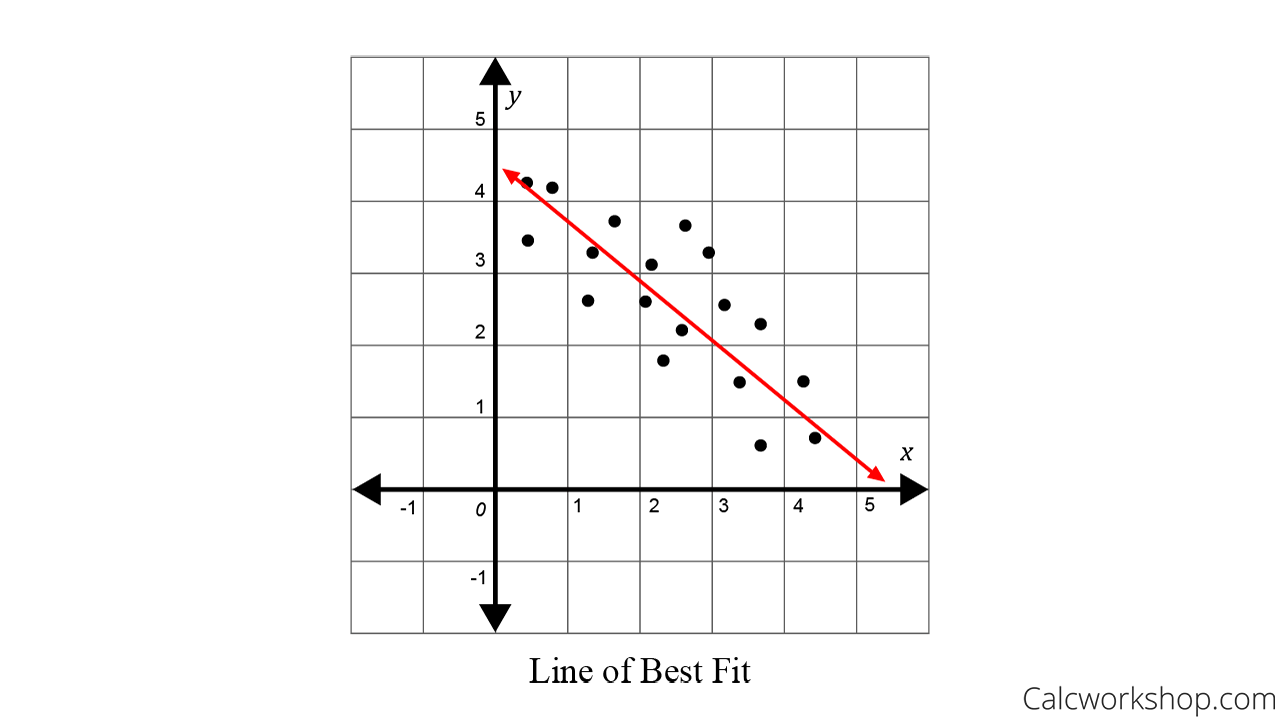
Probability and statistics index > regression analysis > line of best fit. If the slope is given by an integer or decimal value we can always put it over the number 1. A line was fit to the data to model the relationship.

The line of best fit is used to show a trend or correlation between the dependent variable and independent variable (s). Y = mx + b. Then, substitute in the given coordinate and solve for the other coordinate.

The closer the points are to the line of best fit the stronger the correlation is. Y is the dependent variable. M is slope of line;

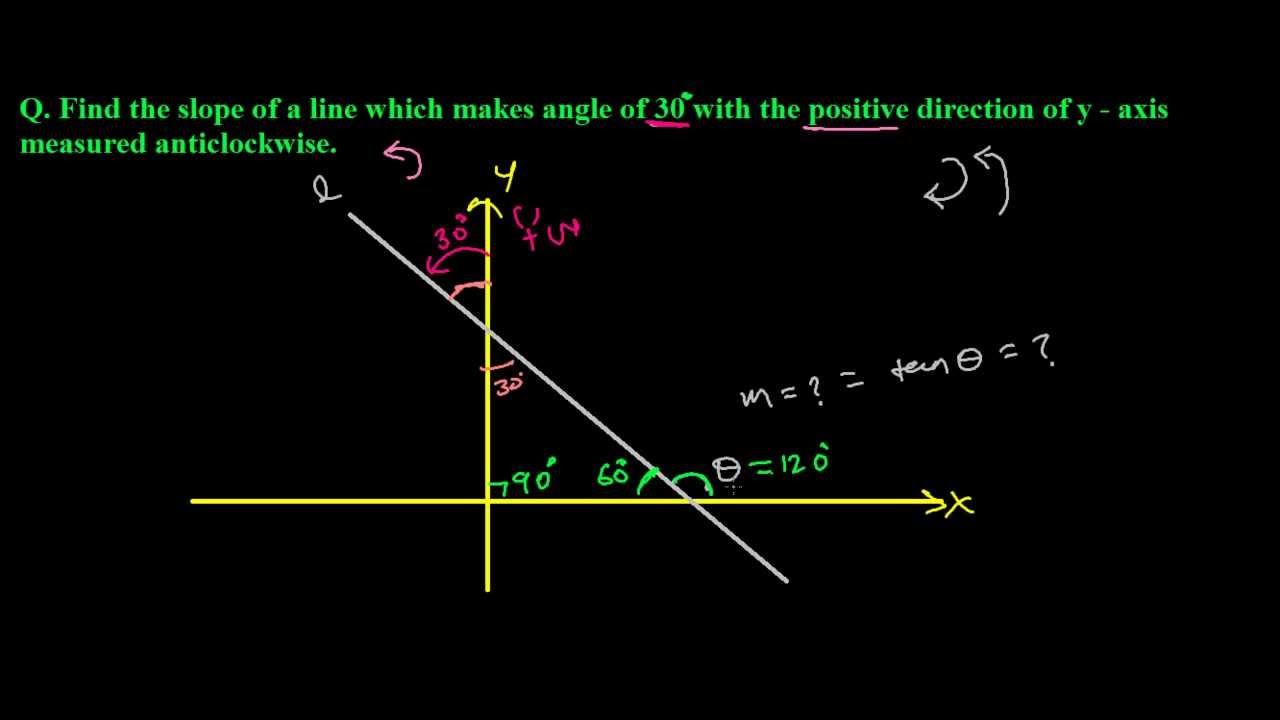
It can be depicted visually, or as a mathematical expression. We can approximate the slope of the line by extending it until we can estimate the [latex]\frac{\text{rise}}{\text{run}}[/latex]. M is the slope of the line.